IMPLANTATION D’ARC DE CERCLE PAR ABSCISSES ET ORDONNÉES SUR TANGENTES SUCCESSIVES
IMPLANTATION D’ARC DE CERCLE PAR ABSCISSES ET ORDONNÉES SUR TANGENTES SUCCESSIVES (l.f.)
Procédé d’IMPLANTATION PAR ABSCISSES ET ORDONNÉES -9,3- d’un arc de cercle défini par un de ses points, la tangente en ce point et son rayon R , dans lequel, en prenant pour base la tangente au point précédent, on détermine l’abscisse et l’ordonnée d’un nouveau point du cercle ainsi que sa tangente.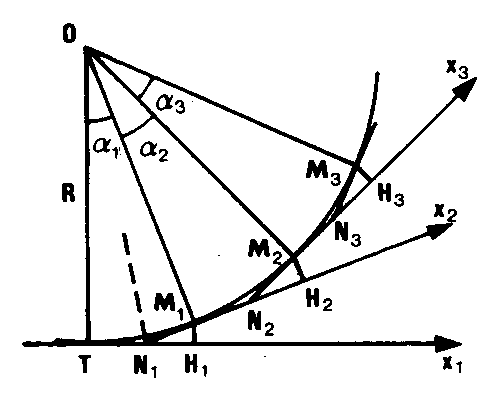 Le premier point M1 est implanté par abscisse et ordonnée sur la tangente Tx1 (1er axe) ainsi que le point N1 de sa tangente :
Le premier point M1 est implanté par abscisse et ordonnée sur la tangente Tx1 (1er axe) ainsi que le point N1 de sa tangente :
Pour M1 : x1 = TH1 = R sin a 1 et y1 = H1M1 = R(1-cos a 1) et pour N1 : x = TN1 = R tan a 1/2
Le deuxième point M2 est implanté par abscisse et ordonnée sur la tangente N1M1x2 en M1 (2ème axe) ainsi que le point N2 de sa tangente; le troisième point M3 est implanté sur la tangente N2M2x3 en M2 (3ème axe) ainsi que le point N3 de sa tangente; etc. On a donc :
Pour M2 : x2 = M1H2 = R sin a 2 et y2 = H2M2 = R(1-cos a 2) et pour N2 : x = M1N2 = R tan a 2/2
– Si l’INTERVALLE ANGULAIRE D’IMPLANTATION a est constant, les « abscisses » et les « ordonnées » sur les tangentes précédentes sont alors constantes.
