IMPLANTATION D’ARC DE CERCLE PAR ABSCISSES ET ORDONNÉES SUR LA TANGENTE (l.f.)
Procédé d’IMPLANTATION PAR ABSCISSES ET ORDONNÉES -9,3- d’un arc de cercle défini par un de ces points, la tangente en ce point et son rayon R, dans lequel, en prenant pour base la tangente, on détermine les « abscisses » et les « ordonnées » de différents points du cercle.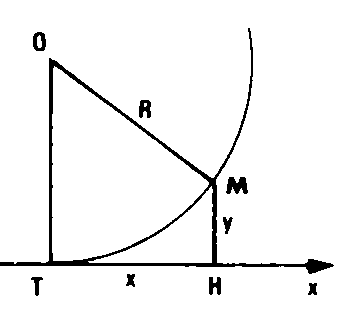– Pour un INTERVALLE ANGULAIRE D’IMPLANTATION quelconque, on se fixe une abscisse arbitraire x = TH sur la tangente et on calcule l’ordonnée y = HM correspondante :
– Pour un INTERVALLE ANGULAIRE D’IMPLANTATION a constant, on calcule : 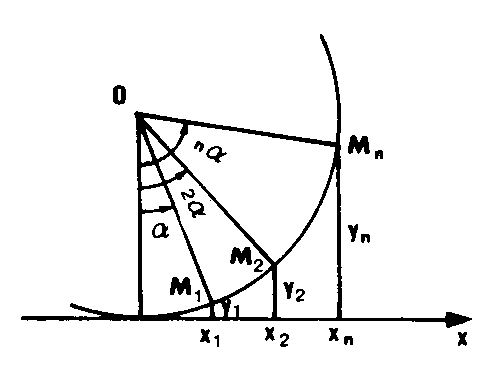Pour M1 : x₁ = R sin a et y₁ = R(1-cos a )
Pour M2 : x₂ = R sin 2a et y₂= R(1-cos 2a ), etc.
Pour Mn : x_n = R sin n a et y_n= R(1-cos n a )