ANGLE DES TANGENTES DE CLOTHOÏDE (l.m.)
Angle que fait la TANGENTE COURTE à l’EXTRÉMITÉ DE CLOTHOÏDE « E. » avec la TANGENTE LONGUE (prolongement de l’alignement droit).
Symb : t
Voir figure ARC DE CLOTHOÏDE. Cet angle, exprime en radions, est : 
avec L : LONGUEUR DE RACCORDEMENT DE CLOTHOÏDE
A : PARAMÈTRE DE CLOTHOÏDE
Re : RAYON DE RACCORDEMENT DE CLOTHOÏDE
Cet angle exprimé en grades est : 
ANGLE POLAIRE DE CLOTHOÏDE (l.m.)
Angle que fait la CORDE DE L’ARC DE CLOTHOÏDE avec le prolongement de l’alignement droit.
Symb : q
Voir figure ARC DE CLOTHOÏDE. Cet angle est très voisin du tiers de l’ANGLE DES TANGENTES DE CLOTHOÏDE t . Exprimé en radian : 
Exprimé en fonction de la LONGUEUR DE RACCORDEMENT « L » et du
PARAMÈTRE DE CLOTHOÏDE « A », il vaut :
ARC DE CLOTHOÏDE (l m.)
Arc d’une CLOTHOÏDE utilisé comme courbe de raccordement progressif entre un alignement droit et un tronçon circulaire, caractérise par le fait que lorsqu’un véhicule le parcourt à vitesse constante, l’angle de braquage des roues varie linéairement en fonction du temps.
L’arc de clothoïde va de l’ORIGINE DE CLOTHOÏDE jusqu’à l’EXTRÉMITÉ DE CLOTHOÏDE. Sa longueur est la LONGUEUR DE RACCORDEMENT DE CLOTHOÏDE « L ».
Cette longueur utile ne dépasse pratiquement pas la valeur du PARAMÈTRE « A » et lui est souvent très inférieure, ce qui justifie les approximations faites en limitant les développements en série des coordonnées paramétriques de la CLOTHOÏDE aux termes donnés pour L < A et même en négligeant le dernier terme si L < A/2.
Pour définir l’arc de clothoïde, il faut connaître deux éléments dont au moins une longueur parmi :
RAYON DE RACCORDEMENT DE CLOTHOÏDE Re
LONGUEUR DE RACCORDEMENT DE CLOTHOÏDE L
PARAMÈTRE DE CLOTHOÏDE A
RIPAGE DE CLOTHOÏDE D R
ANGLE DES TANGENTES DE CLOTHOÏDE t
ANGLE POLAIRE DE CLOTHOÏDE q
Si les deux éléments donnés sont parmi Re, L, A, t , les 2 autres de ces quatre éléments sont liés par des formules simples :
2t = L / Re et L. Re = A²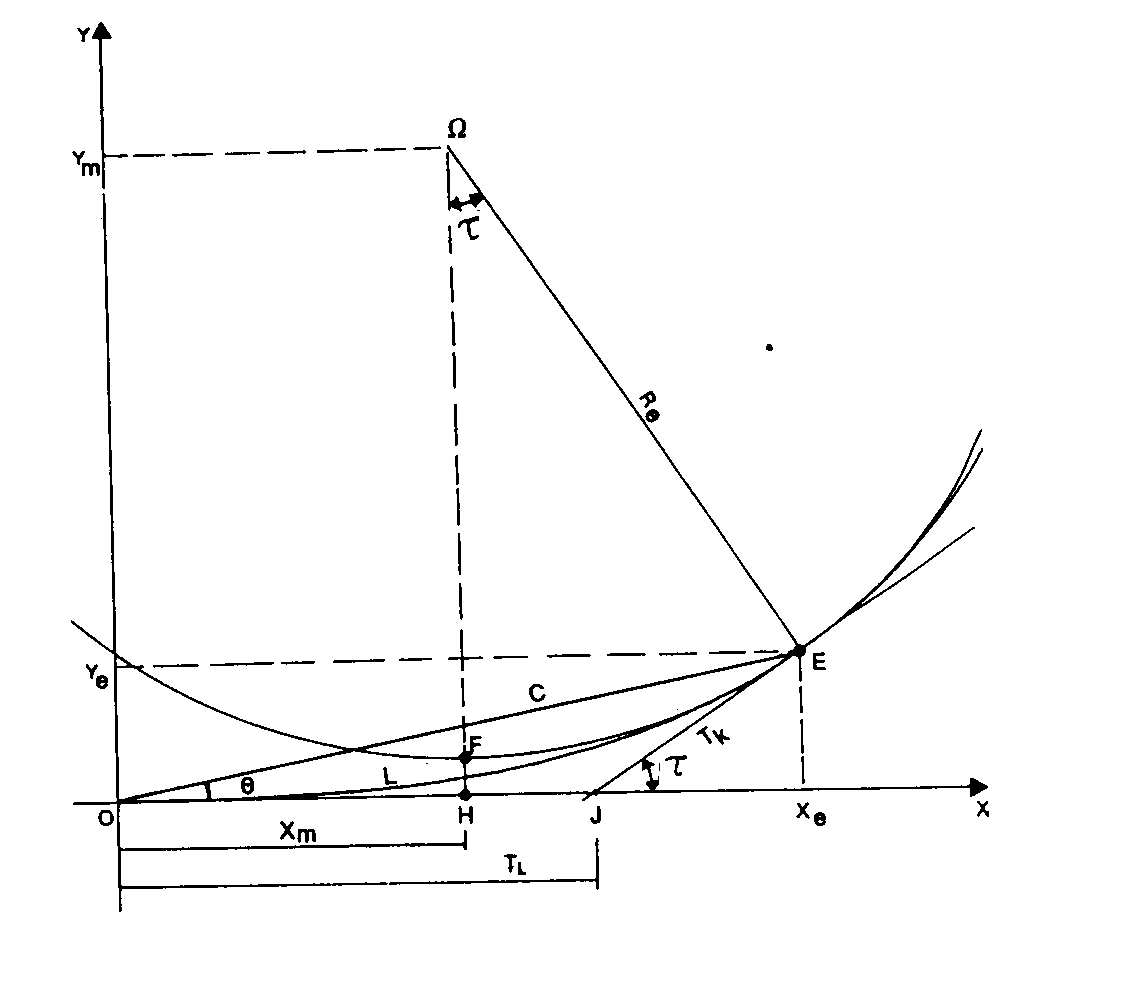
Si par contre le ripage D R est l’un des 2 éléments que l’on souhaite imposer, on aura recours, selon le deuxième élément connu, à l’une des formules approchées suivantes : L² / Re = L3 / A² = A4 / Re3 = 2t .L @ 24 D R
Voir aussi les locutions suivantes :
CERCLE DE RACCORDEMENT DE CLOTHOÏDE CORDE DE L’ARC DE
CLOTHOÏDE C EXTRÉMITÉ DE CLOTHOÏDE E
ORIGINE DE CLOTHOÏDE O
TABLE DE CLOTHOÏDE
TANGENTE COURTE DE CLOTHOÏDE TK
TANGENTE LONGUE DE CLOTHOÏDE TL
ARC DE CLOTHOÏDE ENTRE DEUX CIRCONFÉRENCES (l.m.)
L’ARC DE CLOTHOÏDE est parfois utilisé comme courbe de raccordement progressif entre deux tronçons circulaires :
1 -Si ceux-ci appartiennent à des cercles non sécants, une clothoïde unique pourra raccorder les deux cercles dans les deux cas suivants :
* Les 2 cercles sont intérieurs l’un à l’autre et nécessairement parcourus dans le même sens. L’arc est dit « en œuf » ou en « ove ».
* Les 2 cercles sont extérieurs l’un à l’autre et parcourus en tournant à droite sur l’un, à gauche sur l’autre (courbures opposées, rayons de signes contraires) : l’arc comprendra le point d’inflexion. L’arc est dit « en S » ou « à inflexion ».
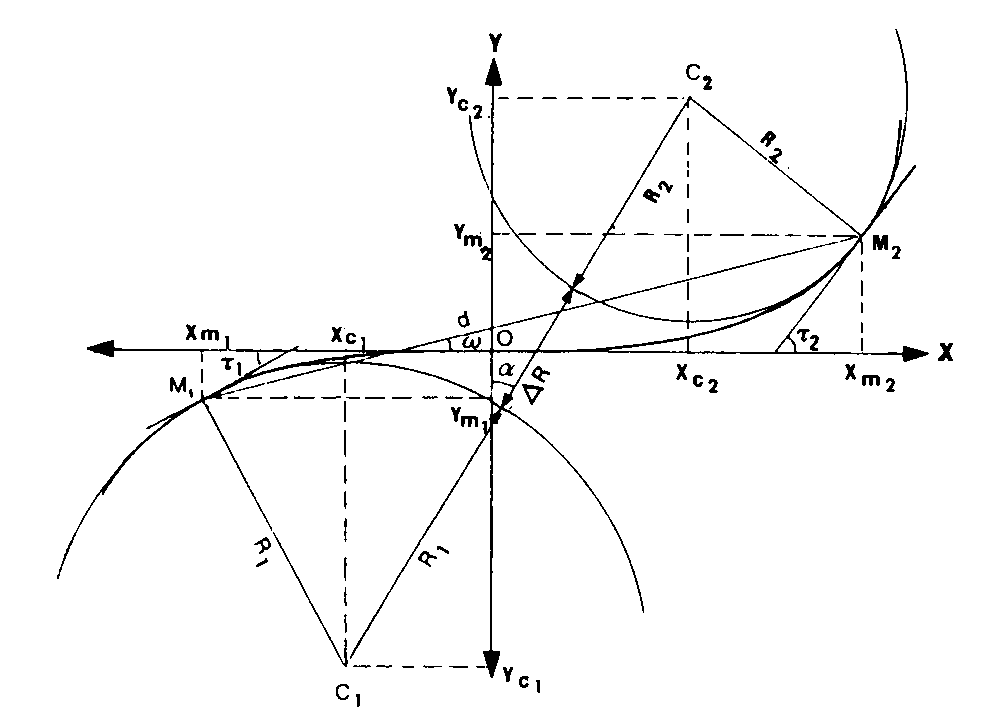
Pour définir l’arc unique de clothoïde de raccordement entre deux circonférences, il faut connaître trois éléments, par exemple les deux rayons R1, R2 et la plus courte distance D R entre les circonférences (Revue XYZ N° 16 d’octobre 1983 : Article de M. José ZELASCO « Clothoïde unique de raccordement entre deux circonférences »).
2 – si ceux-ci appartiennent à 2 cercles sécants ou extérieurs l’un à l’autre et parcourus en tournant dans le même sens, le raccordement ne pourra être assuré qu’avec deux arcs de clothoïde, de même sens de courbure. Si les deux arcs sont contigus, ils se raccordent en un point C où ils doivent avoir nécessairement le même rayon de courbure en admettant un même cercle osculateur, comprenant les cercles à raccorder. Le raccordement est dit « en C » ou « en anse de panier ».
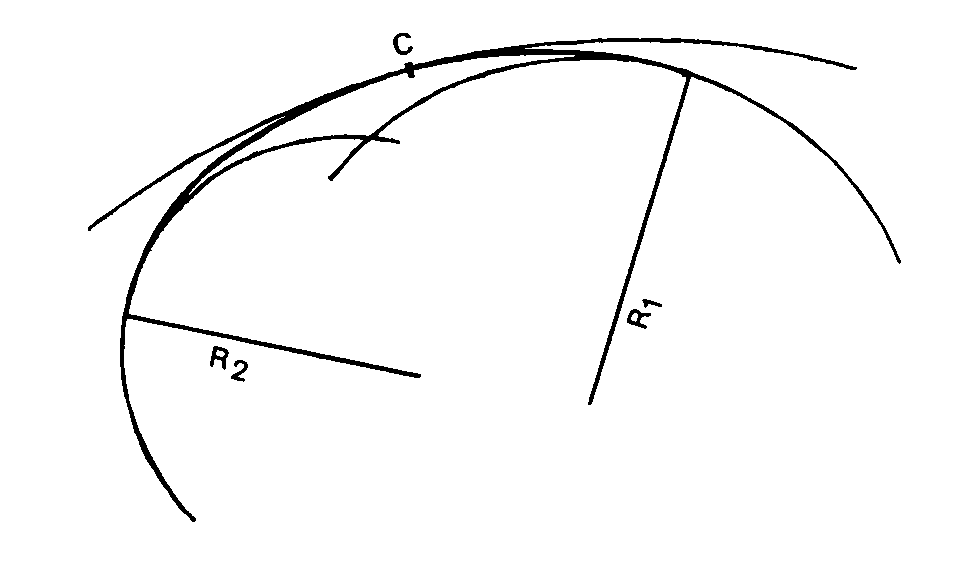
En parcourant le tracé, en C, la variation linéaire de la courbure ne va pas s’arrêter comme lors d’un raccordement à un cercle, mais s’inverser, ce qui n’est pas confortable. Il est alors conseillé d’insérer, si possible, un arc de cercle entre les 2 rayons de clothoïde.
CERCLE DE RACCORDEMENT DE CLOTHOÏDE (l.m.)
Cercle dont le rayon est dit RAYON DE RACCORDEMENT DE CLOTHOÏDE, sur lequel l’ARC DE CLOTHOÏDE vient se raccorder au point EXTRÉMITÉ DE CLOTHOÏDE en lui étant tangent et en ayant le même rayon de courbure ; le cercle de raccordement est osculateur à l’arc de clothoïde.
Les Coordonnées Xm et Ym de son centre W dans le système local de la CLOTHOÏDE sont calculables a partir des coordonnées locales Xe et Ye du point EXTRÉMITÉ DE CLOTHOÏDE et de l’ANGLE DES TANGENTES DE CLOTHOÏDE t :
Xm = Xe – Re sin t
Ym = Ye + Re cos t
L’abscisse Xm est très voisine de la moitié de l’abscisse Xe de l’extrémité de clothoïde. L’ordonnée Ym est très voisine du quart de l’ordonnée Ye de l’extrémité de clothoïde augmenté du rayon Re.
CLOTHOÏDE (n.f.)
Courbe plane dont la courbure (inverse du rayon de courbure) en un point, varie linéairement avec l’abscisse curviligne comptée positivement et négativement de part et d’autre du point ORIGINE DE CLOTHOÏDE pour lequel la courbure est nulle (point d’inflexion).
Autrement dit, en tout point « M » d’une clothoïde le produit du rayon de courbure « R » par l’abscisse curviligne « S » est constant : R x S = Constante.
Cette constante est homogène au carré d’une longueur « A » appelée PARAMÈTRE DE LA CLOTHOÏDE : R x S = A²
Au point M d’abscisse curviligne « S », le cercle de rayon R ayant même tangente que la clothoïde lui est osculateur ; autrement dit, les deux courbes passent par le même point, ont la même tangente et ont le même rayon de courbure. La clothoïde est extérieure au cercle osculateur vers l’ORIGINE DE LA CLOTHOÏDE, intérieure au cercle du côté opposé.
En un point quelconque d’une clothoïde, le cercle osculateur contient, sans les toucher, tous les cercles osculateurs aux points d’abscisse curviligne supérieure. Une clothoïde ne peut donc admettre comme osculateurs, deux cercles sécants.
Toutes les clothoïdes sont homothétiques entre elles, à une symétrie près par rapport à la tangente au point origine, et en particulier, dans le rapport A, avec la clothoïde « unitaire » de paramètre A = l .
CLOTHOÏDE ( ÉQUATION DE LA ) (l.f.)
La CLOTHOÏDE, de PARAMÈTRE A, peut être définie dans un système de oordonnées locales, de centre « O » ORIGINE DE CLOTHOÏDE, l’axe Ox étant la droite tangente à la courbe en ce point, par différentes équations :
1 – Coordonnées rectangulaires paramétriques de la clothoïde en fonction de l’abscisse curviligne S :
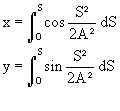en développant en série et en intégrant :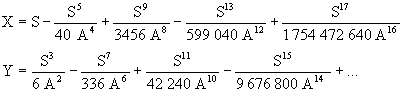
2 – Coordonnées polaire paramétriques de la clothoïde en fonction de l’abscisse curviligne S :
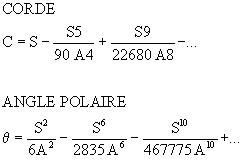Toutes ces formules convergent assez rapidement et permettent un calcul relativement facile avec une calculatrice programmable de poche.
3 – Équation cartésienne de la clothoïde :
Sous cette forme, on voit que la clothoïde est très voisine de la parabole cubiqueosculatrice au point origine :
CORDE DE L’ARC DE CLOTHOÏDE (l.f.)
Segment de droite OE joignant l’ORIGINE DE CLOTHOÏDE « O » a l’EXTRÉMITÉ DE CLOTHOÏDE « E ».
Symb: C
Voir figure ARC DE CLOTHOÏDE
Sa longueur peut s’exprimer par un développement en fonction :
– de la LONGUEUR DE RACCORDEMENT DE CLOTHOÏDE L
– du PARAMÈTRE DE CLOTHOÏDE A
EXTRÉMITÉ DE CLOTHOÏDE (l.f.)
Point de contact entre l’ARC DE CLOTHOÏDE de raccordement et le CERCLE DE RACCORDEMENT DE CLOTHOÏDE.
Symb : E
Ses coordonnées Xe et Ye dans le système local de la clothoïde sont calculables en fonction de la LONGUEUR DE RACCORDEMENT L et du PARAMÈTRE A par les formules paramétriques de la CLOTHOÏDE. Elles sont aussi données dans les TABLES DE CLOTHOÏDE.
IMPLANTATION D’UN ARC DE CLOTHOÏDE (l.f.)
Pour IMPLANTER -9,l- un ARC DE CLOTHOÏDE, on se donne l’alignement droit et l’ORIGINE DE CLOTHOÏDE O et 2 éléments, généralement le RAYON DE RACCORDEMENT DE CLOTHOÏDE Re et la LONGUEUR DE RACCORDEMENT L.
Les divers autres éléments sont donnés par les TABLES DE CLOTHOÏDE, mais il est plus aisé d’en faire le calcul avec une calculatrice programmable de poche.
* Avec une TABLE DE CLOTHOÏDE on obtiendra :
– le PARAMÈTRE DE CLOTHOÏDE A,
– l’abscisse Xm du centre W du CERCLE DE RACCORDEMENT DE CLOTHOÏDE,
– le RIPAGE DE CLOTHOÏDE D R dont on déduit l’ordonnée Ym du centre W du cercle de raccordement de rayon Re : Ym = D R + Re,
– l’ANGLE DES TANGENTES DE CLOTHOÏDE t ,
– l’abscisse Xe et l’ordonnée Ye de l’EXTRÉMITÉ DE CLOTHOÏDE E,
– la TANGENTE COURTE : TK = JE,
– la TANGENTE LONGUE : TL = OJ.
* Avec une calculatrice programmable, on calculera dans l’ordre à l’aide de formules :
– le PARAMÈTRE , 
– l ‘ANGLE DES TANGENTES DE CLOTHOÏDE
(en radian)
– les coordonnées locales de l’EXTRÉMITÉ DE CLOTHOÏDE Xe et Ye par les développements en série,
– les coordonnées locales du centre W du CERCLE DE RACCORDEMENT DE CLOTHOÏDE Xm et Ym : Xm = Xe – Re sin t et Ym = Ye + Re cos t
– le RIPAGE DE CLOTHOÏDE D R = Ym – Re,
– la TANGENTE LONGUE TL = Xe – Ye cotan t
– la TANGENTE COURTE TK = Ye / sin t
L’IMPLANTATION -9,1- de ces différents éléments pourra se faire par une polygonale O H J E W F H, (voir figure ARC DE CLOTHOÏDE), sans calcul des coordonnées terrain :
– sur le prolongement de l’alignement de gisement Ga on porte les longueurs OH = Xm et OJ = TL,
– du point J on porte sur la direction de gisement Ga – t , la longueur JE = TK,
– du point E on porte sur la direction de gisement Ga – t – 100 grades, la longueur EW = Re,
– du point W on porte sur la direction de gisement Ga + 100 grades, les longueurs W F = Re et W H = Ym et l’on constatera que l’on retrouve bien le point H déjà implanté,
– si le centre W est inaccessible, on implantera éventuellement le point F directement à partir de E en portant sur la direction de gisement Ga – t /2 + 200 grades, la longueur EF = 2 Re sin t /2.
IMPLANTATION D’UN ARC DE CLOTHOÏDE (POINTS DE DÉTAIL) (l.f.).
Les formules paramétriques polaires de la CLOTHOÏDE permettent de calculer, pour un point quelconque M de la courbe, la CORDE DE L’ARC DE CLOTHOÏDE OM et l’ANGLE POLAIRE DE CLOTHOÏDE q en fonction de l’abscisse curviligne S, et de procéder ainsi à l’IMPLANTATION PAR RAYONNEMENT -9,3- en plaçant la STATION D’IMPLANTATION -9,1- au point « O » ORIGINE DE CLOTHOÏDE et en prenant le prolongement de l’alignement comme RÉFÉRENCE -1,1-.
Si on souhaite garder un INTERVALLE LINÉAIRE D’IMPLANTATION « i » -9,4- constant, on peut utilement recourir à l’IMPLANTATION SEMI-POLAIRE -9,3- : on procède à L’OUVERTURE DES ANGLES -9,1- polaires successifs, qui sont pratiquement en progression géométrique, et on implante chaque point à la distance constante du précédent par un simple CHAÎNAGE -2,2-.
Cette méthode peut également être mise en œuvre en plaçant la STATION D’IMPLANTATION -9,1- au point « E » EXTRÉMITÉ DE CLOTHOÏDE, avec comme direction de RÉFÉRENCE -1,1- la TANGENTE COURTE : les angles polaires successifs doivent simplement être augmentés d’autant de fois la moitié de l’arc capable sous-tendu sur le cercle de raccordement par le segment constant, qu’il y a de segments depuis le départ. 
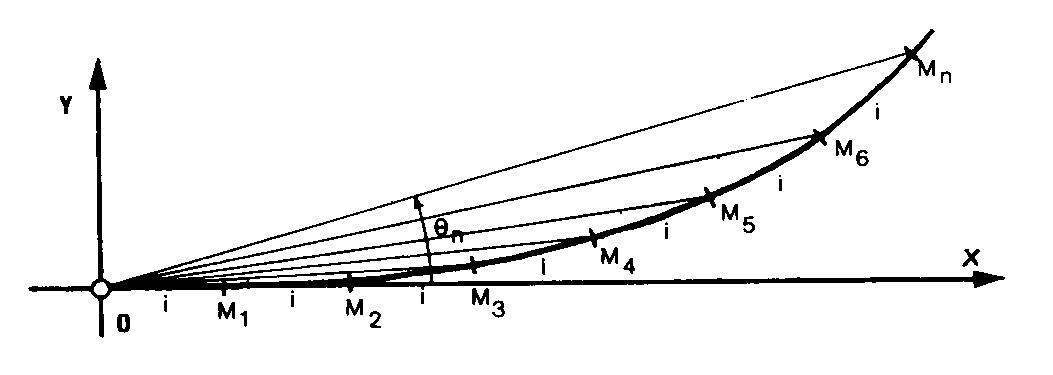
LONGUEUR DE RACCORDEMENT DE CLOTHOÏDE (l.f.)
Longueur de L’ARC DE CLOTHOÏDE OE entre l’ORIGINE DE CLOTHOÏDE « O » et L’EXTRÉMITÉ DE CLOTHOÏDE « E ».
Symb : L.
Voir figure ARC DE CLOTHOÏDE.
C’est l’abscisse curviligne « S » de l’extrémité de clothoïde.
ORIGINE DE CLOTHOÏDE (l.m.)
Point de la clothoïde où la courbure est nulle (rayon de courbure infini).
Symb : O
Ce point est un point d’inflexion et de symétrie de la courbe : la courbure est positive d’un côté, négative de l’autre. La droite tangente à la clothoïde en ce point est osculatrice.
Lorsque la clothoïde est utilisée comme courbe de raccordement entre un alignement droit et un cercle, le point origine de la clothoïde marque nécessairement l’extrémité de l’alignement droit et l’origine de L’ARC DE CLOTHOÏDE.
PARAMÈTRE DE CLOTHOÏDE (l.m.)
Longueur « A » qui, par définition de la CLOTHOÏDE, lie le rayon de courbure « R » de la clothoïde en un point quelconque M à la longueur « S » de l’arc OM depuis
l’ORIGINE DE CLOTHOÏDE (abscisse curviligne) : Symb : A, par la relation : R x S = A² ou R x S = – A², selon qu’en parcourant la clothoïde à partir du point origine, on tourne à gauche (R positif) ou à droite (R négatif).
Dans ce dernier cas, les valeurs de
– l’ANGLE DES TANGENTES DE CLOTHOÏDE t ,
– l’ANGLE POLAIRE DE CLOTHOÏDE q ,
– l’ordonnée de l’EXTRÉMITÉ DE CLOTHOÏDE Ye,
changent de signe car dans leur expression, tous les dénominateurs où figurent uniquement des puissances impaires de la quantité [A²] devant être changé en [- A²], changent eux-mêmes de signe.
En O, S = O et R ® infini. En E, S = L et Re = A²/L
Pour un ARC DE CLOTHOÏDE, le paramètre est choisi en fonction de différents critères et arrondi par excès à une valeur pour laquelle il existe des gabarits de traçage à l’échelle du projet.
RAYON DE RACCORDEMENT DE CLOTHOÏDE (l.m.)
Rayon du CERCLE DE RACCORDEMENT DE CLOTHOÏDE au point EXTRÉMITÉ DE CLOTHOÏDE « E ». Symb : Re
Voir figure ARC DE CLOTHOÏDE.
Par convention on considère comme positif le rayon d’un cercle parcouru dans le sens trigonométrique, c’est-à-dire en tournant à gauche, et comme négatif, et on lui affectera le signe -, le rayon d’un cercle parcouru dans l’autre sens, en tournant à droite.
RIPAGE DE CLOTHOÏDE (l.m.)
Distance à l’alignement droit, du point « F » du CERCLE DE RACCORDEMENT DE CLOTHOÏDE qui en est le plus proche.
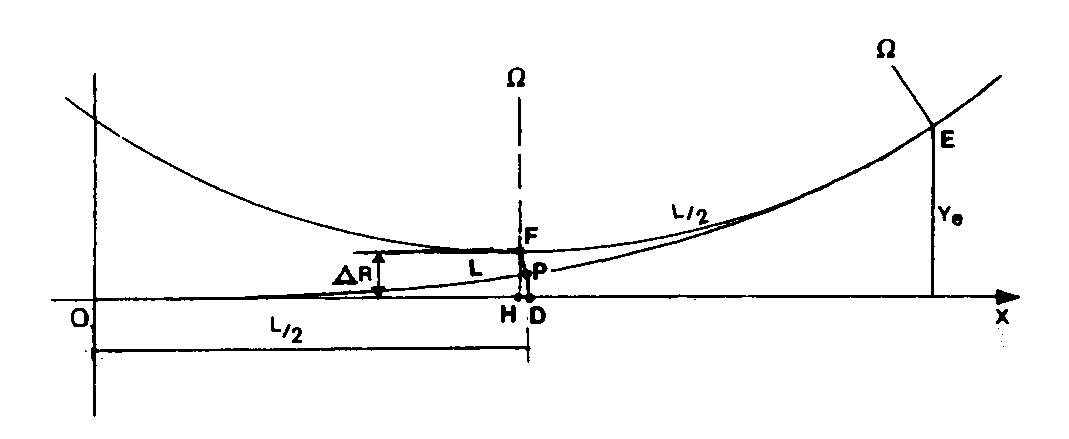
D R = HF , Arc EF = L/2 , OD = L/2
Le ripage de clothoïde vaut très sensiblement le quart de l’ordonnée Ye de l’EXTRÉMITÉ DE CLOTHOÏDE.
L’ARC DE CLOTHOÏDE OE passe sensiblement au milieu du segment HF. Il passe encore plus exactement au milieu « P » du segment DF, le point « D » étant sur le prolongement de l’alignement, à la distance L/2 de l’ORIGINE DE CLOTHOÏDE, comme le point F est sur le cercle de raccordement à l’abscisse curviligne L/2 de l’extrémité « E » de clothoïde, l’arc EF du cercle valant exactement en effet la moitié de la LONGUEUR DE RACCORDEMENT « L » de l’arc de clothoïde. Les points D et P milieu du segment DF méritent d’être implantés pour servir de contrôle à l’IMPLANTATION DE L’ARC DE CLOTHOÏDE
TABLE DE CLOTHOÏDE (l.f.)
Table donnant, pour toute une série d’ARCS DE CLOTHOÏDE numérotés, les valeurs de :
L’intervalle tabulaire est tel qu’on peut interpoler linéairement entre deux clothoïdes consécutives.
TANGENTE COURTE DE CLOTHOÏDE (l.f.)
Segment EJ de la tangente à l’EXTRÉMITÉ DE CLOTHOÏDE » E « , compris entre cette extrémité et l’alignement droit prolongé.
Symb : TK
Voir figure ARC DE CLOTHOÏDE.
La tangente courte vaut sensiblement le tiers de l’arc de clothoïde.
TANGENTE LONGUE DE CLOTHOÏDE (l.f.)
Segment OJ de l’alignement droit prolonge, compris entre l’ORIGINE DE CLOTHOÏDE « O » et le point « J » d’intersection de la tangente à l’l’EXTRÉMITÉ DE CLOTHOÏDE.
Symb : TL
Voir figure ARC DE CLOTHOÏDE.
La tangente longue vaut sensiblement les 2/3 de l’arc de clothoïde.