IMPLANTATION PAR ABSCISSES ET ORDONNÉES (l.f.)
IMPLANTATION -9,1- de points à partir de deux POINTS D’IMPLANTATION -9,1- formant une LIGNE D’OPÉRATION -2,2-, en reportant des distances sur cette ligne et perpendiculairement à cette ligne. C’est l’opération inverse du procédé de LEVER PAR ABSCISSES ET ORDONNÉES -2,6-.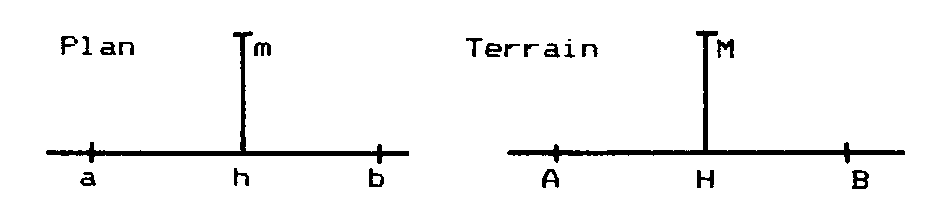 
Au point H tel que AH = ah.E (E dénominateur de l’ÉCHELLE -1.1-), on élève la perpendiculaire HM sur laquelle on porte la longueur HM = hm.E au ruban. On utilise soit L’ÉQUERRE OPTIQUE -2,6-, soit le TACHÉOMÈTRE -7,1- pour matérialiser les angles droits tels que AHM.
Pour implanter une courbe, on calcule d’abord les « abscisses » et les « ordonnées » des différents points que l’on reporte comme ci-dessus.
IMPLANTATION PAR DISTANCES (BIPOLAIRES LINÉAIRES) (l.f)
IMPLANTATION -9,1- d’un point A, à partir des distances à 2 POINTS D’IMPLANTATION -9,1- B et C, le segment BC étant LIGNE D’OPÉRATION -2,2-.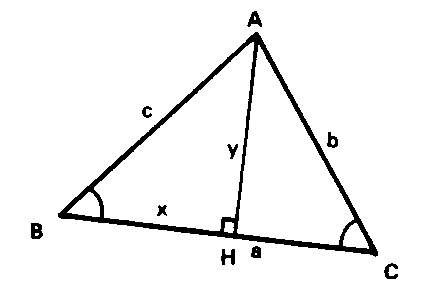 
Les longueurs des 3 côtés triangle ABC sont mesurées sur le plan ou déduites des coordonnées de A, B et C. Si on désigne les distances correspondantes sur le terrain, réduites à l’horizon, par :
a = BC, b = AC, c = AB, on calcule :
– 1ère méthode : IMPLANTATION PAR ABSCISSE ET ORDONNÉE du point A : 
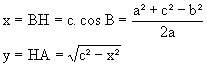– 2ème méthode : IMPLANTATION PAR RAYONNEMENT du point A :
En B, depuis le côté BC, on procède à L’OUVERTURE DE L’ANGLE B -9,1- et, dans cette direction, on implante le point A à la distance c.
– 3ème méthode : IMPLANTATION PAR INTERSECTION du point A :
On calcule également l’angle C : 
En B et C, depuis le côté BC, on procède à L’OUVERTURE DES ANGLES B et C -9.1- et on intersecte ainsi le point A.
IMPLANTATION PAR INTERSECTION (l.f.)
IMPLANTATION -9,1- d’un point connu en coordonnées par OUVERTURES D’ANGLE -9,1- au théodolite, en deux (ou plusieurs) STATIONS D’IMPLANTATION -9,1- connues (S1, S2…).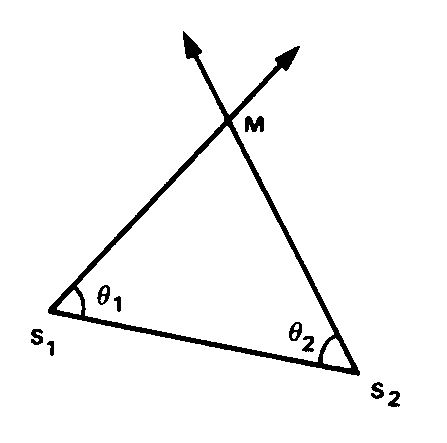
A cet effet on calcule les GISEMENTS -3,5- entre les stations d’une part, telles que S1S2 et entre station et le point à implanter d’autre part, tel que S1M, S2M. On déduit par différence les angles q 1 , q 2 ,… qui permettent l’implantation du point en utilisant deux ou plusieurs théodolites simultanément. Un aide procède au PIQUETAGE -1,1- des points a l’intersection des visées.
IMPLANTATION PAR RAYONNEMENT (l.f.)
IMPLANTATION -9,1- par OUVERTURE D’UN ANGLE -9,1- en une STATION D’IMPLANTATION -9,1- et report de la DISTANCE D’IMPLANTATION -9,1-.
C’est l’opération inverse du procédé de RAYONNEMENT PLANIMÉTRIQUE -3,8-.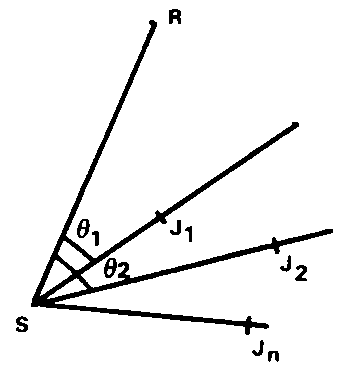 
En une station d’implantation S à partir des angles polaires q 1 , q 2 , … , q i … et des distances polaires r1 = SJ1, r2 = SJ2, … ri = SJi … calculés, on implante les points J1 , J2 … Ji … en procédant à l’OUVERTURE DES ANGLES -9,1- à partir de la RÉFÉRENCE -1,1- SR et par report des distances.
On dit aussi « Implantation polaire ».
IMPLANTATION POLAIRE (l.f.)
Voir IMPLANTATION PAR RAYONNEMENT
IMPLANTATION SEMI-POLAIRE (l.f.)
IMPLANTATION – 9,1- d un point par OUVERTURE D’UN ANGLE -9,1- en une STATION D’IMPLANTATION -9,1- et par une DISTANCE D’IMPLANTATION -9,1- à partir d’un POINT IMPLANTE -9,1-, généralement voisin.
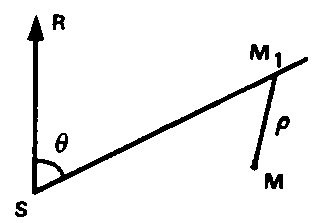
Cette méthode est commode pour implanter des points successifs M1 , M2 , M3 ,… régulièrement espacés sur un cercle ou un ARC DE CLOTHOÏDE -9,5-, l’INTERVALLE LINÉAIRE D’IMPLANTATION -9,4- entre les points, constant et court, pouvant être assuré par CHAÎNAGE -2,2- .