COEFFICIENT DE RÉDUCTION -1,4- à appliquer aux longueurs mesurées.
On distingue :
Coefficient d’étalonnage. voir ÉTALONNAGE DES INSTRUMENTS DE MESURE DE DISTANCE.
Coefficient de réduction à l’horizon. voir RÉDUCTION A L’HORIZON.
Coefficient de réduction à l’ellipsoïde. voir RÉDUCTION A l’ellipsoïde.
Coefficient d’altération linéaire. voir ALTÉRATION LINÉAIRE -10,2-.
Coefficient de réduction d’échelle : terme impropre, à remplacer par module de réduction, voir RÉDUCTION D’ÉCHELLE -10,2-.
COEFFICIENTS DE RÉDUCTION DES LONGUEURS (l.m.)
CORRECTIONS AUX LONGUEURS (l.f.) CORRECTIONS -1,4- que l’on apporte aux longueurs mesurées.On distingue :
Correction d’anallatisme. voir ANALLATISME -7,1-.
Correction d’étalonnage. voir ÉTALONNAGE DES INSTRUMENTS DE MESURE DE DISTANCE.
Correction de réduction à l’horizon. voir RÉDUCTION A L’HORIZON.
Correction de réduction à l’ellipsoïde. voir RÉDUCTION A L’ELLIPSOÏDE.
Correction d’altération linéaire. voir ALTÉRATION LINÉAIRE -10,2-.
DISTANCE RÉDUITE A L’HORIZON (l.f.)
Longueur de la projection verticale A’M’ d’une distance RM sur la surface de niveau du point I d’altitude moyenne entre A et M.
Symb : Dh
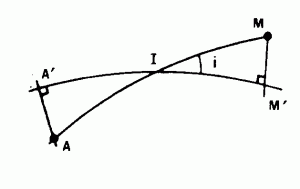
ZI = (ZA + ZM) / 2
où ZI, ZA, ZM sont les altitudes respectives de I, R, M.
Voir RÉDUCTION A L’HORIZON.
DISTANCE RÉDUITE A LA PROJECTION (l.f.)
Symb : Dr
Voir RÉDUCTION A LA PROJECTION -10,2-.
DISTANCE RÉDUITE A L’ELLIPSOÏDE
Symb : Do
Longueur de la projection verticale d’une longueur Dp = AM sur l’ellipsoïde de référence : Do = AoMo.
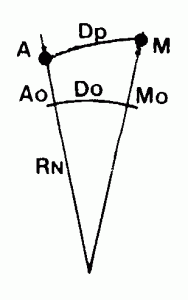
Si on désigne par hA et hM les auteurs de A et M au-dessus de l’ellipsoïde de référence et par D h la dénivelée : D h = hM – hA, on a
Do² = (Dp² – D h²) / [(1 + hA / RN ).(1 + hM / RN )]
RN rayon de courbure moyen de l’ellipsoïde sur la ligne A M
En première approximation, on peut souvent prendre R = 6 370 km.
Le calcul de Do peut se faire aussi en deux temps :
a) calcul de Dh (voir RÉDUCTION A L’HORIZON)
b) calcul de Do à partir de Dh (voir RÉDUCTION à L’ELLIPSOÏDE)
ÉTALONNAGE DES INSTRUMENTS DE MESURE DE DISTANCE (module, coefficient, correction d’)
1) ÉTALONNAGE (n.m.)
Pour un instrument de mesure de distances, opération consistant à mesurer la longueur d’une BASE D’ÉTALONNAGE, et à comparer le résultat B, à la distance connue BE de cette base.
2) MODULE D’ÉTALONNAGE (l.m.)
Quotient mE entre la longueur BE d’étalonnage et la longueur B mesurée avec l’instrument considéré.
mE = BE / B
3) COEFFICIENT D’ÉTALONNAGE (l.m.)
Quantité (BE – B) / B = mE – 1 ; c’est la correction par unité de longueur.
4) CORRECTION D’ÉTALONNAGE. Correction cE qu’il y a lieu d’apporter à la quantité D mesurée avec un instrument étalonné :
DCOR = D + CE
La correction d’étalonnage s’obtient en multipliant la distance D mesurée par le COEFFICIENT D’ÉTALONNAGE KE.
cE = KE.D
MODULES DE RÉDUCTION DES LONGUEURS : MODULES DE RÉDUCTION -1,4- à appliquer aux longueurs mesurées.
On distingue :
Module d’étalonnage : voir ÉTALONNAGE DES INSTRUMENTS DE MESURE DE DISTANCE.
Module de réduction à l’horizon : voir RÉDUCTION A L’HORIZON.
Module de RÉDUCTION à l’ellipsoïde : voir RÉDUCTION A L’ELLIPSOÏDE.
Module de réduction à la projection : voir RÉDUCTION A LA PROJECTION et ALTÉRATION LINÉAIRE -10,2-.
Module de réduction d’échelle : voir RÉDUCTION D’ÉCHELLE -10,2-.
RÉDUCTION A L’HORIZON (module, coefficient, correction de réduction à l’horizon)
1) RÉDUCTION A L’HORIZON (l.f.) A partir d’une distance Dp entre deux points A et B, mesurée selon la pente, calcul permettant d’obtenir :
* la DISTANCE HORIZONTALE Dh lorsqu’on réduit à l’horizontale rectiligne du point de station A.
H projection orthogonale de B sur l ‘horizontale de A
Dh = Dp cos i
* la DISTANCE RÉDUITE A L’HORIZON A’B’ à l’altitude moyenne entre les deux extrémités A et B de la visée.
A’B’ # AB cos i’
Dh # Dp cos i’
A’ et B’ projections verticales de A et B sur la surface de niveau passant par I
2) MODULE DE RÉDUCTION A L’HORIZON (l.m.) : mh Quotient entre la distance réduite à l’horizon Dh et la distance mesurée selon la pente Dp :
mh = Dh / Dp = cos i (= sin z)
mh est toujours inférieur à 1
3) COEFFICIENT DE RÉDUCTION A L’HORIZON (l.m.) : kh
kh = (Dh – Dp) / Dp = mh – 1
Il est toujours négatif. C’est la correction par unité de longueur à apporter à la distance mesurée selon la pente pour obtenir la distance réduite à l’horizon.
4) CORRECTION DE RÉDUCTION A L’HORIZON (l.f.)
Correction Co à apporter à la distance mesurée selon la pente Dp pour obtenir la distance réduite à l’horizon Dh, correction toujours négative.
Dh = Dp + ch avec ch = kh Dp
RÉDUCTION A L’ELLIPSOÏDE (module, coefficient, correction de réduction à l’ellipsoïde)
1) RÉDUCTION A L’ELLIPSOÏDE (l.f.) A partir d’une distance entre deux points, calcul permettant d’obtenir la distance homologue Do sur l’ellipsoïde de référence.
La réduction à l’ellipsoïde peut être effectuée :
* directement à partir de la DISTANCE SELON LA PENTE -2,1-. Voir DISTANCE RÉDUITE A L’ELLIPSOÏDE.
* par l’intermédiaire de la DISTANCE RÉDUITE A L’HORIZON Dh. Dans ce cas seulement on définit les quantités 2.3.4 ci-après.
2) MODULE DE RÉDUCTION A L’ELLIPSOÏDE (l.m.)
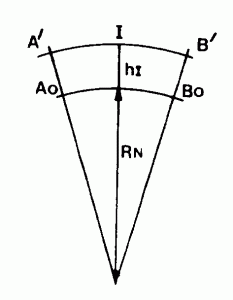
Soit A’B’ une distance réduite à l’horizon, Ao et Bo les projections verticales de A’ et B’ sur l’ellipsoïde de référence. On appelle module de réduction à l’ellipsoïde le quotient de Do = AoBo par :
DhAB = A’B’
mo = Do / DhAB = RN / ( RN + HI) = # 1 – HI / RN
RN : rayon de courbure moyen de l’ellipsoïde sur la ligne Ao Bo,
hI : hauteur de A’B’ au dessus de l’ellipsoïde.
3) COEFFICIENT DE RÉDUCTION A L’ELLIPSOÏDE (l.f.)
Symb : ko
ko = (Do – DhAB) / DhAB = mo – 1 autrement dit, c’est la correction par unité de longueur à apporter à la distance réduite à l’horizon pour obtenir la distance sur l’ellipsoïde. Elle est négative, pour les distances entre deux points situés au dessus de l’ellipsoïde.
4) CORRECTION DE RÉDUCTION A L’ELLIPSOÏDE (l.f.) Correction Co à apporter à la distance déjà réduite à l’horizon : Dh, pour obtenir la distance homologue sur l’ellipsoïde de : Do.
Do = Dh + Co avec Co = ko Dh
RÉDUCTION DES LONGUEURS (l.f.) partir d’une longueur donnée, calcul permettant d’obtenir une autre longueur de même nature et voisine.
Voir : RÉDUCTION A L’HORIZON -2,5-
RÉDUCTION A L’Ellipsoïde
RÉDUCTION A LA PROJECTION -10,2-
RÉDUCTION D’ECHELLE
