Catégories du lexique : 10.7 Compensation - Ajustement planimétrique

ADAPTATION (n.f.)
Cadastre : Méthode de calcul transformant un réseau géométrique (dans un système national), avec des déformations aussi faibles que possible.

AJUSTEMENT (n.m.)
Procédé simplifié de répartition des écarts, permettant d’obtenir des résultats homogènes en évitant le recours aux méthodes de COMPENSATION PAR LES MOINDRES CARRÉS. Exemples :
* Ajustement d’un cheminement,
* Ajustement logarithmique d’une chaîne de triangulation,
* Ajustement graphique d’une intersection ou d’un relèvement.

AJUSTEMENT ANGULAIRE D’UN CHEMINEMENT (l.m.)
Mode de répartition de l’ÉCART DE FERMETURE ANGULAIRE D’UN CHEMINEMENT -10,5- goniométrique sur ses différents angles. Voir RÉVERSIBILITÉ D’UN CHEMINEMENT.
Si  » fa  » est l’écart de fermeture,  » n  » le nombre de côtés et  » n+1  » le nombre d’angles observés, chaque angle reçoit la correction : – fa/n+1

AJUSTEMENT EN ABSCISSES ET ORDONNÉES D’UN CHEMINEMENT (l.m.)
Mode de répartition des ÉCARTS DE FERMETURE D’UN CHEMINEMENT EN ABSCISSE ET ORDONNÉES « fX, fY » -10,5-, sur les différentes coordonnées d’un cheminement planimétrique.

1 – Ajustement parallèle simple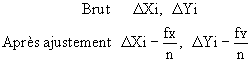Ce type d’ajustement est utilisé lorsque les côtés du cheminement sont sensiblement égaux.

2 – Ajustement parallèle proportionnel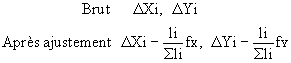avec
D Xi = XMi – X Mi-1
D Yi = YMi – YMi-1
li = Mi-1 Mi (longueur du côté de rang i)

3) Ajustement par rotation et variation d’échelle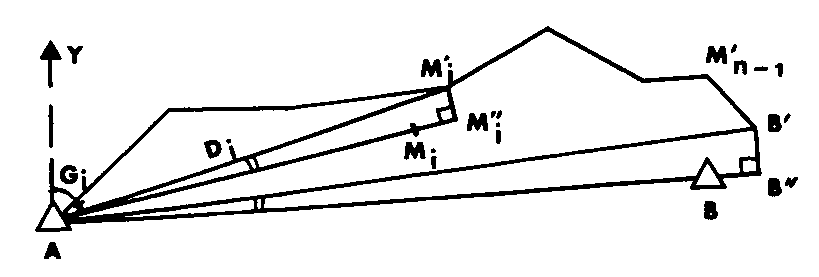Posons AM’i = Di
Pour ramener le point B’ sur le point connu B, on considère le coefficient de rotation q et le coefficient d’échelle p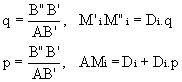Posons
D XMi = XM’i – XA = Di sin Gi
D YMi = YM’i – YA = Di cos Gi

en différentiant :

d(D XMi) = dDi sin Gi + Di cos Gi . dGi
d(D YMi) = dDi cos Gi – Di sin Gi . dGi
et avec dDi = p.Di et dGi = q , on a les corrections d’ajustement :

d(D XMi) = p. D Xmi + q. D YMi
d(D YMi) = p. D Ymi – q. D XMi

AJUSTEMENT GRAPHIQUE (l.m.)
Méthode de détermination des corrections à apporter en abscisse et en ordonnées aux coordonnées d’un point approché « M0 », par un GRAPHIQUE D’AJUSTEMENT.
Cette méthode est souvent désignée à tort par MÉTHODE DU POINT APPROCHÉ, appellation trop imprécise, puisque toute méthode d’ajustement graphique, d’ajustement par le calcul ou de compensation par les moindres carrés fait appel à un point approché.

AJUSTEMENT GRAPHIQUE D’UN RECOUPEMENT (l.m.)
Ayant obtenu les coordonnées d’un point approche Mo par RECOUPEMENT (CALCUL D’UN) -10,4-, on trace les visées relatives à A et B passant par Mo et, au voisinage de Mo, la visée de gisement GMC observée. On procède ensuite comme s’il s’agissait d’un AJUSTEMENT GRAPHIQUE D’UNE INTERSECTION.

AJUSTEMENT GRAPHIQUE D’UN RELÈVEMENT (l.m.)
Ayant obtenu les coordonnées d’un point approché Mo par RELÈVEMENT SUR TROIS POINTS -10,4-, on trace les SEGMENTS CAPABLES -10,4- (voir GISEMENT D’UN SEGMENT CAPABLE -10,4-), puis tenant compte de leurs déplacement (voir DÉPLACEMENT D’UN SEGMENT CAPABLE -10,4-), on trace au rapporteur les C2n segments capables qui se coupent en C3n POINTS TRIPLES -10,4-.
On trace les BANDES DE SENSIBILITÉ et on détermine le point définitif « M » par – AJUSTEMENT GRAPHIQUE.

AJUSTEMENT GRAPHIQUE D’UNE INSERTION (l.m.)
L’INSERTION -3,7- combinant des VISÉES D’INTERSECTION -3,7-, des SEGMENTS CAPABLES -10,4- de relèvement, des SEGMENTS DISTANCE -10,4- de multilatération, ces différents lieux géométriques sont tracés sur un GRAPHIQUE D’AJUSTEMENT comme précisé dans les méthodes d’AJUSTEMENT GRAPHIQUE indiquées à propos de ces trois procédés.

AJUSTEMENT GRAPHIQUE D’UNE INTERSECTION (l.m.)
Ayant obtenu les coordonnées d’un point approche Mo par INTERSECTION (CALCUL D’) -10,4-, on trace sur un GRAPHIQUE D’AJUSTEMENT les différentes visées d’intersection et leurs BANDES DE SENSIBILITÉ -10,4-. On détermine le point définitif « M » par AJUSTEMENT GRAPHIQUE.

AJUSTEMENT GRAPHIQUE D’UNE MULTILATÉRATION (l.m.)
Ayant obtenu les coordonnées d’un point approché Mo par BILATÉRATION (CALCUL DE) -10,4-, on trace sur un GRAPHIQUE D’AJUSTEMENT les BANDES D’INDÉCISION -10,4- des différents SEGMENTS DISTANCE -10,4- pour lesquels on aura calculé le DÉPLACEMENT (D’UN SEGMENT DISTANCE) -10,4-. On détermine le point définitif « M » par AJUSTEMENT GRAPHIQUE.

AJUSTEMENT LOGARITHMIQUE (l.m.)
Méthode d’ajustement qui permet de rendre linéaire une équation de condition aux côtés, en passant aux logarithme (décimaux ou népériens).

AJUSTEMENT LOGARITHMIQUE POUR L’ACCORD DES BASES DANS UNE CHAÎNE DE TRIANGLES (l.m.)
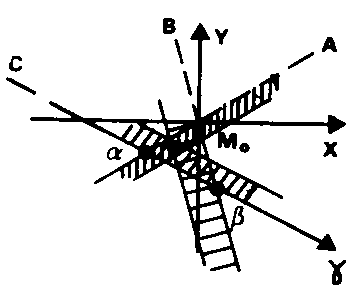
Exemple avec 5 triangles : On désigne par b et g les angles adjacents aux côtés périphériques et par a les angles intérieurs.
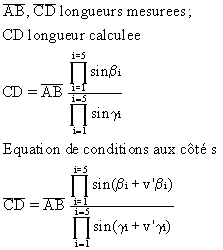
Voir ÉQUATION DE CONDITION AUX CÔTÉS DANS UNE CHAÎNE DE TRIANGLES POUR L’ACCORD DES BASES. On rend cette équation linéaire en passant aux logarithmes népériens et en écrivant :où v’b i est exprimé en milligrades.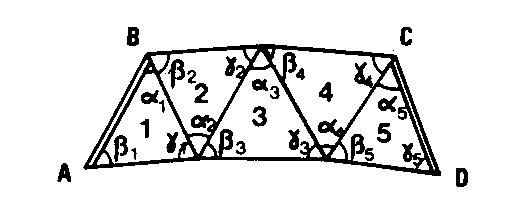Une solution est donnée par la relation (1) :

v’b 1 = v’b 2 = … v’b i = … v’b n et
v’g 1 = v’g 2 = … v’g i = … v’g n = – v’b i

Angles satisfaisant à la fois aux conditions aux angles des triangles et aux côtés.

1er ajustement :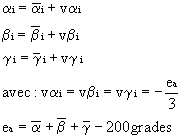2ème ajustement :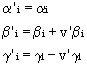avec v’b i donné par relation (1) précédente.

COMPENSATION (n.f.)
Traitement numérique d’observation en surnombre, ou de quantités qui s’en déduisent directement, en vue d’obtenir une valeur unique pour chaque grandeur à déterminer.

COMPENSATION PAR LES MOINDRES CARRÉS (l.f.)
Compensation qui rend minimum la somme des carrés des résidus S vi².

COMPENSATION PAR LES MOINDRES CARRÉS AUX ÉQUATIONS DE CONDITION (l.f.)
Méthode de compensation dans laquelle on s’impose des conditions qui, jointes à la condition S vi² minimum, permettent de calculer les valeurs compensées des observations. Les conditions imposées se traduisent par des ÉQUATIONS DE CONDITION.

COMPENSATION PAR LES MOINDRES CARRÉS PAR VARIATION DE COORDONNÉES (l.f.)
Méthode de compensation qui fournit directement, comme résultat du calcul, les variations de coordonnées qui permettent, à partir des coordonnées des points approchées, d’obtenir les coordonnées des points définitifs.

COMPENSATION PAR LES MOINDRES CARRÉS PAR VARIATION DE GISEMENT (l.f.)
Méthode de compensation qui fournit directement comme de résultat les variations de gisement qui permettent, à partir des gisements provisoires, d’obtenir les gisements définitifs.

COMPENSATION PLANIMÉTRIQUE À PARTIR D’UN POINT APPROCHÉ (l.f.)
Compensation numérique d’observations en surnombre qui fournit les coordonnées définitives d’un point à partir de celles d’un point approché.
L’opération graphique correspondante constitue un AJUSTEMENT GRAPHIQUE, expression préférable à celle de MÉTHODE DU POINT APPROCHÉ.

DOOLITLE (ALGORITHME DE) (l.m.)
Algorithme de calcul permettant de résoudre un système de plusieurs ÉQUATIONS NORMALES par la méthode de substitution.

ÉQUATION DE CONDITION AUX ANGLES DANS UN TRIANGLE (l.f.)

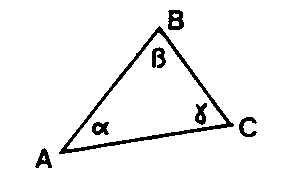
Soient :

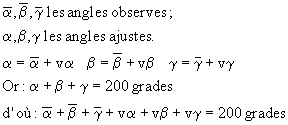
Posons :

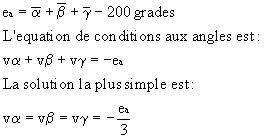
ÉQUATION DE CONDITION AUX ANGLES DANS UNE CHAÎNE DE TRIANGLES POUR L’ACCORD DES GISEMENTS (l.f.)

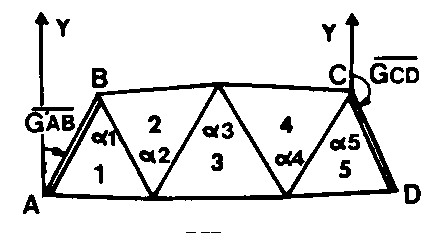Exemple avec 5 triangles :
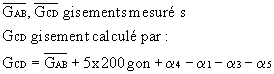Équation de condition aux angles

Une solution est :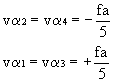Il faut aussi calculer les nouveaux angles ajustés b et g , assurant l’équation aux angles dans chaque triangle.
Lorsqu’on veut réaliser à la fois l’accord des gisements et celui des bases AB et CD, il faut d’abord calculer les angles ajustés assurant l’accord des gisements et l’équation aux angles dans chaque triangle, puis calculer par AJUSTEMENT LOGARITHMIQUE les angles ajustés assurant l’accord des bases. (Voir aussi ÉQUATION DE CONDITION AUX CÔTÉS DANS UNE CHAÎNE DE TRIANGLES POUR L’ACCORD DES BASES).

ÉQUATION DE CONDITION AUX CÔTÉS DANS UNE CHAÎNE DE TRIANGLES POUR L’ACCORD DES BASES (l.f.)

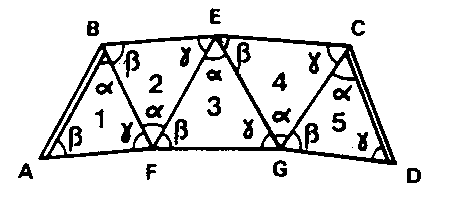
Exemple avec 5 triangles :

ÉQUATION NORMALE (l.f.)
Dans la compensation par les moindres carrés, équation obtenue en différentiant la somme des carrés des expressions des résidus par rapport à une variable.
Chaque expression de résidu correspond à une relation d’observation. Il y a autant d’équations normales qu’il y a d’inconnues.

GRAPHIQUE D’AJUSTEMENT (l.m.)
Dans la détermination des coordonnées d’un point isolé, graphique à grande ÉCHELLE -1,1- permettant, à partir des coordonnées d’un point approché Mo, de tracer un certain nombre de lieux géométriques de détermination du point, dont certains sont surabondants.
L’échelle du graphique peut être comprise entre 1/1 et 1/50.
Ces lieux servent d’axes à des BANDES DE SENSIBILITÉ ou des BANDES D’INDÉCISION -10,4- dont le recouvrement permet le choix le plus rationnel du point définitif M, sans recourir à la méthode de COMPENSATION PAR LES MOINDRES CARRÉS.
Pour obtenir les coordonnées de M, on mesure graphiquement les différences de coordonnées entre Mo et M. Voir AJUSTEMENT GRAPHIQUE et POINT APPROCHÉ (MÉTHODE DU).

Exemple de graphique d’ajustement appliqué à une INTERSECTION -10,4- :
Soit une intersection dont 1e point approché Mo(Xo,Yo) a été calculé à partir des points A et B. Soit à tracer la visée issue d’un troisième point C, de gisement Gcm :

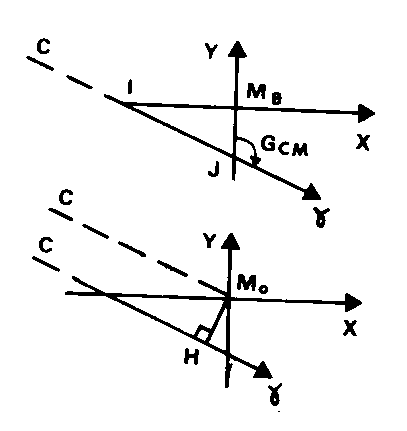
lère méthode : on calcule, selon l’orientation de la visée, l’une des deux coordonnées :
Xi = Xc + (Yo – Yc )tan Gcm,
Yj = Yc + (Xo – Xc)cotan Gcm,
et l’on trace au rapporteur par I ou par J la direction Ig de gisement Gcm .

2ème méthode : On calcule

et l’on fait la différence dG = Gcm – Gcmo.
La visée de gisement Gcm passe à la distance MoH de Mo telle que
MoH = CM.dG (rad ) ou MoH = CM.dG(mgon).1,57.10-5

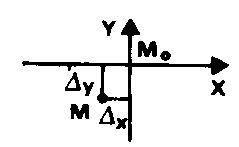
Le graphique d’ajustement consiste à tracer en outre par Mo les visées AMoa et BMob de gisements Gamo et Gbmo formant le CHAPEAU -10,4- Moa b .
On dessine ensuite les demi-bandes de sensibilité vers l’intérieur du chapeau, de largeurs proportionnelles aux SENSIBILITÉS DES VISÉES D’INTERSECTION -10,4-, se recouvrant selon un petit triangle à l’intérieur duquel on choisit la position du point M ajusté. On mesure à l’échelle choisie, par exemple 1/5, les différences de coordonnées D X et D Y entre Mo et M, d’où :
Xm = Xo – D X et Ym = Yo – D Y

HATT (MÉTHODE DE) (l.f.)
Voir AJUSTEMENT GRAPHIQUE D’UN RELÈVEMENT.

LAPLACE (RELATION DE) (l.f.)
La relation de Laplace donne la différence entre l’AZIMUT GÉODÉSIQUE  » Az g  » -3,6- d’une direction et l’AZIMUT ASTRONOMIQUE  » Az a  » -3,6- de cette même direction.
Az a – Az g = (l a – l g) sin j a avec

l a LONGITUDE ASTRONOMIQUE
l g LONGITUDE GÉODÉSIQUE
j a LATITUDE ASTRONOMIQUE

La relation de Laplace permet de calculer l’azimut géodésique d’un côté situé à l’extrémité d’une chaîne de triangulation, à partir de l’azimut astronomique observé correspondant : à cet azimut, « Az g » dit observé, correspond un gisement observé « V obs », qui intervient dans la RELATION D’OBSERVATION EN VARIATION DE COORDONNÉES RELATIVE A UNE OBSERVATION D’AZIMUT ASTRONOMIQUE.
On appelle CORRECTION DE LAPLACE, la quantité :
C Laplace = Az g – Az a

NORMALISATION (n.f.)
Opération qui consiste à passer des RELATIONS D’OBSERVATIONS aux ÉQUATIONS NORMALES.

POINT APPROCHÉ (MÉTHODE DU) (l.f.)
La méthode désigne un procédé utilisant un GRAPHIQUE D’AJUSTEMENT pour la détermination d’un point isolé par INTERSECTION, RELÈVEMENT, RECOUPEMENT, INSERTION -3,7- et MULTILATÉRATION -2,6-, à partir d’un point approché.
Comme toute méthode d’AJUSTEMENT GRAPHIQUE, d’ajustement par le calcul ou de COMPENSATION PAR LES MOINDRES CARRÉS, on utilise les coordonnées d’un point approché.
L’appellation  » méthode du point approché  » est trop imprécise et il y a lieu de lui substituer celle d’AJUSTEMENT GRAPHIQUE.

RELATION D’OBSERVATION EN VARIATION DE COORDONNÉES RELATIVE À UNE OBSERVATION D’AZIMUT ASTRONOMIQUE (l.f.)
Relation liant la variation de gisement « dGi », due a des variations dX, dY des coordonnées des extrémités de la visée, le gisement observé issu de l’azimut astronomique « G obs », le gisement calcule « G calc », et le résidu « vi ».

dGi – G obs + G calc = vi

Le gisement observé est déduit de l’azimut astronomique en effectuant la correction de Laplace (voir LAPLACE (RELATION DE), puis en tenant compte de la CONVERGENCE DU MÉRIDIEN -10,2- et de la RÉDUCTION ANGULAIRE À LA CORDE (CORRECTION DE) -10,2-.

RELATION D’OBSERVATION EN VARIATION DE COORDONNÉES RELATIVE À UNE OBSERVATION DE DIRECTION (l.f.)
Relation liant la variation de gisement « dGi » à des variations de coordonnées dX, dY des extrémités des visées, le gisement provisoire calculé à partir du point approché « Gcalc », le gisement observé provisoirement orienté « Gobs », la variation du Go de station « dGo » et le résidu « vi ».

dGi – G obs + G calc – dGo= vi

expression générale dans laquelle dGi se calcule par :

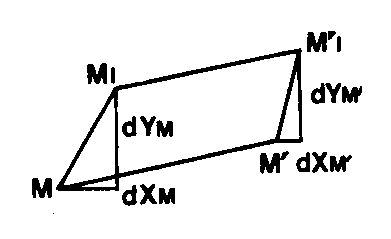
D X = XM’ – XM
D Y = YM’ – YM
D = MM’

Cas particulier d une intersection :
dXM = dYM = 0
dG0 = 0:

RELATION D’OBSERVATION EN VARIATION DE COORDONNÉES RELATIVE À UNE OBSERVATION DE DISTANCE (l.f.)
Relation liant la variation  » dGi  » due à des variations de coordonnées dX, dY des coordonnées des extrémités, la distance provisoire calculée à partir de points approchés  » D calc « , la distance observée  » D obs  » et le résidu  » vi « .

dDi – D obs + D calc = vi

avec :

dDi = – dXMsinG – dYMcosG + dXM’sinG + dYM’cosG

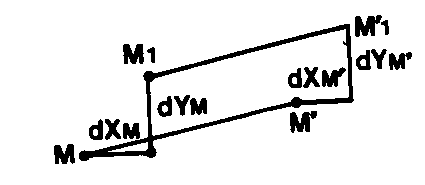
G gisement de MM’

RÉSIDU (n.m.)
Correction qu’il faut apporter à une mesure Xi pour avoir la valeur la plus plausible Xm, ou la valeur compensée définitive X def.
Symb : vi
Xm = Xi + vi avec Xm, moyenne arithmétique de n valeurs mesurées.
X def = Xi + vi avec X def, valeur compensée définitive de X.