BANDE D’INDÉCISION (l.f.)
Bande d’un GRAPHIQUE D’AJUSTEMENT -10,7- dans laquelle se trouve un SEGMENT DISTANCE. Cette bande est située de part et d’autre de la position calculée du segment distance et sa largeur est proportionnelle à l’erreur commise sur la distance.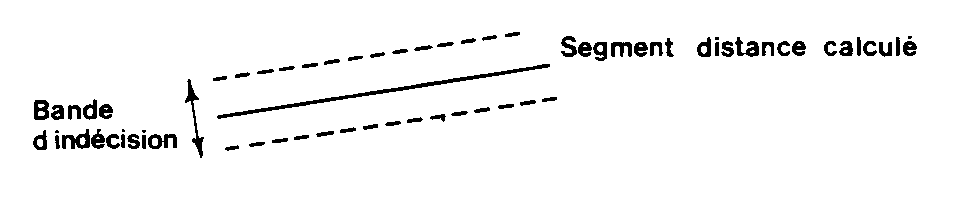
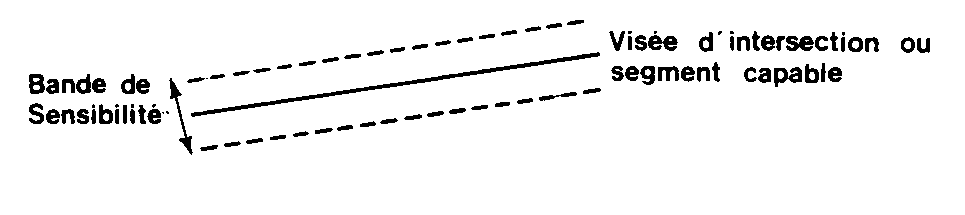
BANDE DE SENSIBILITÉ (l.f.)
Bande d’un GRAPHIQUE D’AJUSTEMENT -10,7- dans laquelle se trouve une visée d’intersection ou un SEGMENT CAPABLE. Cette bande est située de part et d’autre de la position calculée et sa largeur est proportionnelle à la SENSIBILITÉ.
BILATÉRATION (CALCUL DE ) (l m.)
On connaît les coordonnées de A et B (XA XB, XB YB) et les distances mesurées DA, DB. On calcule :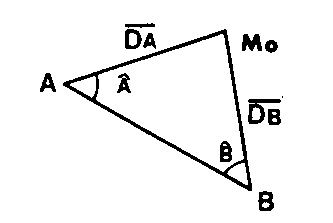
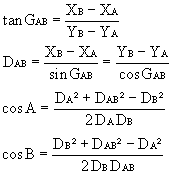
d’où :
GAMo = GAB – A
GBMo = GAB + B + 200 grades et
Xo = XA + DA sin GAMo ou Xo = XB + DB sin GBMo
Yo = YA + DA cos GAMo ou Yo = YB + DB cos GBMo
La vérification s’effectue par la mesure d’au moins une troisième distance Dc = CM. La bilatération est un procédé de calcul du point approché Mo d’une MULTILATÉRATION -2,6-, ou plus généralement d’une INSERTION -3,7-.
CHAPEAU (n.m.)
Ensemble des lieux géométriques :
VISÉES D’INTERSECTION, SEGMENTS CAPABLES, SEGMENTS DISTANCES qui, dans un GRAPHIQUE D’AJUSTEMENT -10,7-, ne concourent pas.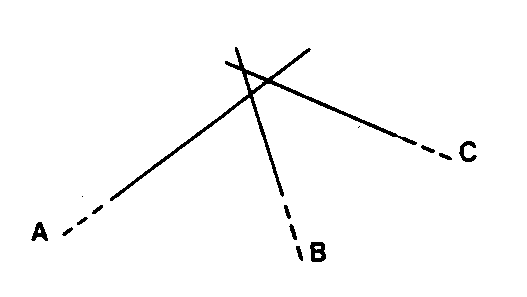
Exemple : chapeau d’un graphique d’ajustement d’intersection.
DÉPLACEMENT D’UN SEGMENT CAPABLE (l.m.)
Produit de la SENSIBILITÉ D’UN SEGMENT CAPABLE, par la différence entre l’angle de relèvement observé a i et l’angle de relèvement calculé a i cal, à partir des coordonnées du point approché.
Symb : dc
dc (cm) = 0,1 . s(cm) . da i (mgon) avec da i = a i – a i calc
DÉPLACEMENT D’UN SEGMENT DISTANCE (l.m.)
Différence obtenue en retranchant à la distance observée, la distance calculée à partir des coordonnées du point approché.
Symb. : dd
dd = D obs – D calc
DISTANCE FICTIVE D’UN SEGMENT CAPABLE (l.f.)
Produit des distances du point approché Mo aux deux points d’appui A et B, divisé par la distance séparant ces deux points.
Symb. : DfAB
avec DA = MoA, DB = MoB, DAB = AB
DÉPLACEMENT D’UNE VISÉE D’INTERSECTION (l.m.)
Produit de la SENSIBILITÉ DE LA VISÉE D’INTERSECTION par la différence entre le gisement observé et le gisement calcule à partir du point approché.
Symb. : di
di (cm) = 0,1 . s (cm) . dG (mgon)
ÉCART D’ORIENTATION DE STATION (l.m. )
1 – Écart angulaire entre le gisement observé et le gisement définitif d’une direction.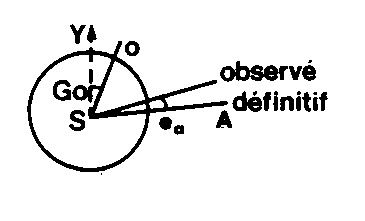
2 – Écart angulaire entre le Go moyen d’un tour d’horizon et le Go pour cette direction.
Voir GISEMENT DU ZÉRO DU LIMBE POUR UNE DIRECTION et GISEMENT DU ZÉRO DU LIMBE POUR UN TOUR D’HORIZON -3,5-.
eo = GSA obs – GSA déf
eo = Go – Gom
ÉCART EN DISTANCE D’UN POINT DE CANEVAS D’ENSEMBLE ORDINAIRE (l.m.)
Sur un GRAPHIQUE D’AJUSTEMENT -10,7-, distance entre le point définitif et l’un des lieux géométriques de détermination : visée d’intersection, SEGMENT CAPABLE, SEGMENT DISTANCE.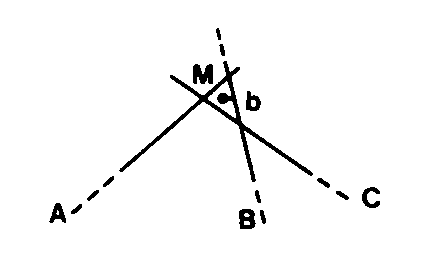
Ex. : Écart en distance de la visée d’intersection issue de B : Mb.
ÉCART-TYPE D’ORIENTATION DE STATION (l.m.)
(Réglementation) Moyenne quadratique des écarts individuels d’orientation : s G
GISEMENT D’UN SEGMENT CAPABLE (l.m.)
Gisement du SEGMENT CAPABLE obtenu après le calcul du point approché Mo d’un RELÈVEMENT SUR TROIS POINTS.
Symb. : GAB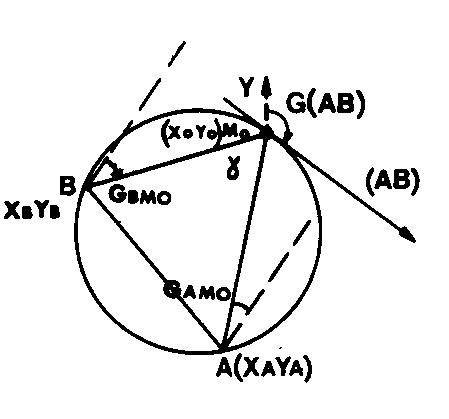
On calcule successivement :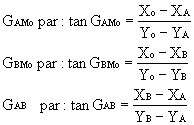
On a G(AB) = GAMo + GBMo – GAB
INTERSECTION (CALCUL D’) (l.m.)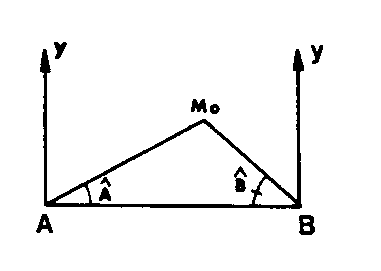
Calcul du point approché :
l – On donne les angles observés en A et B : A = BAMo B = ABMo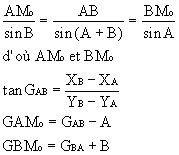
Xo = XA + AMo sin GAMo
Yo = YA + AMo cos GAMo
Xo = XB + BMo sin GBMo
Yo = YB + BMo cos GBMo
2 – On donne les gisements de AMo (GAMo) et de BMo (GBMo)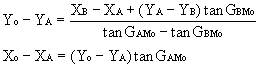
INTERSECTION SPATIALE (CALCUL D’) (l.f.)
Détermination dans l’espace à trois dimensions de l’intersection de deux ou plusieurs visées orientées, issues d’autant de station S1, S2, …, Si…
On calcule les cosinus directeurs de chaque visée à partir de son GISEMENT -3,5- et de son ANGLE ZÉNITHAL -4,31-, puis le carré Di² de la distance de la visée issue de Si à un point M (XYZ).
La COMPENSATION PAR LES MOINDRES CARRÉS de la somme des carrés tels que Di² donne la solution (Voir Revue XYZ N°11 de juin 1982, article de Robert VINCENT).
POINT TRIPLE (l.m.)
Sur un GRAPHIQUE D’AJUSTEMENT -10,7- relatif à .un RELÈVEMENT, point de concours de trois SEGMENTS CAPABLES non indépendants. Lorsqu’on a affaire à un relèvement sur « n » points, il y a Cnp points triples.
Ex. n = 4, C43 = 4
RECOUPEMENT (CALCUL D’UN) (l.m.)
Voir le principe du RECOUPEMENT -3,7- .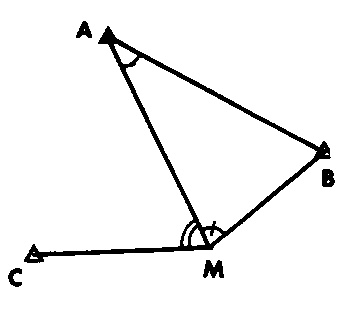
Points connus A , B et C.
Angles observés, en A : BAM, en M : CMA et AMB. On calcule le gisement AB :
et on déduit les gisements :GAM = GAB + BAM
GMB = GMA + AMB
d’où : GBM = GAM + AMB
et on obtient M par CALCUL D’INTERSECTION.
Le point C n’intervient que que pour la vérification : on calcule le gisement de MC à partir des coordonnées de M et de C et on vérifie que sa différence avec le gisement de MA est bien égale à l’angle observé CMA.
RELÈVEMENT SUR TROIS POINTS (CALCUL D’UN) (l.m.)
1 – MÉTHODE DE DELAMBRE.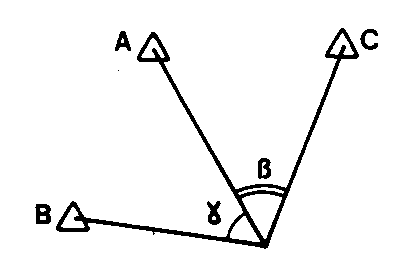
On calcule d’abord :
On en déduit : GMoB = GMoA – g
On calcule ensuite les coordonnées de Mo par intersection à partir de A et B avec les gisements GAMo et GBMo. Voir INTERSECTION (CALCUL D’).
Dans la formule donnant GMoA on prend cotan (- g ) car les angles (MoA, MoC) = b et (MoA, MoB) = g ont des signes opposés sur la figure. Si ces deux angles ont même signe, remplacer – g par g .
2 – Méthode faisant intervenir sur les deux arcs capables ABM et ACM, les points B’ et C’ diamétralement opposés à A, choisi provisoirement comme origine des coordonnées.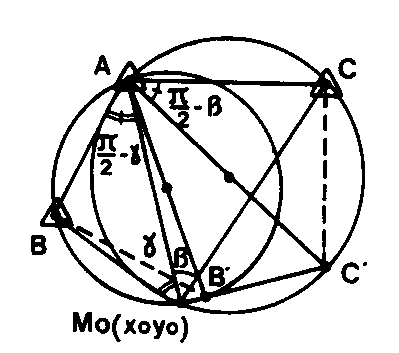
XB’ = XB – YB cotan g et YB’ = YB + YB cotan
XC’ = XC + YC cotan b et YC’ = YC – XC cotan b
On pose :
D² = (XC’ – XB’)² + (YC’ – YB’)²
a = |XB’ YC’ – XC’ YB’|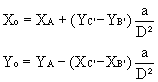
3 – RELÈVEMENT ITALIEN.
Le procédé revient a calculer 2 intersections successives.
a) Calcul des coordonnées de N , qui est le point de rencontre de MoC et du cercle circonscrit à ABMo par intersection à partir de A et de B avec les angles : 200 grades – a en A et b en B. Voir INTERSECTION (CALCUL D’).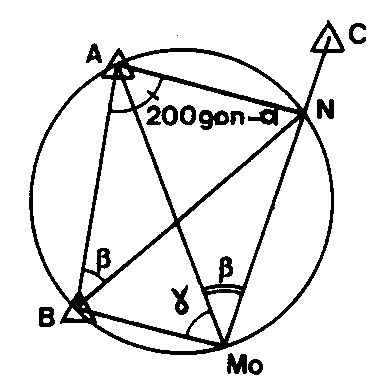
Les coordonnées de N permettent le calcul du gisement de NC :
Or, GMoC = GNC d’où : GMoA = GMoC – b
GAMo = GMoA + 200 grades
et GCMo = GNC – 200 grades
b) Deuxième calcul d’intersection à partir de A et de C avec les gisements connus GAMo et GCMo.
Voir INTERSECTION (CALCUL D’).
4 – RELÈVEMENT BARYCENTRIQUE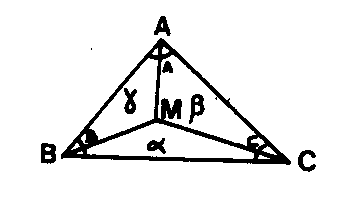
A, B, C angles déduits par différences de gisements,
a , b , g angles observés en M.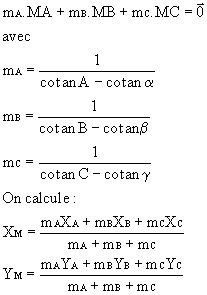
SEGMENT CAPABLE (l.m.)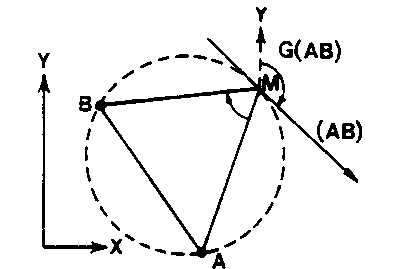
Tangente orientée à l’arc capable de l’angle de relèvement, au voisinage du point à déterminer, traitée comme une visée d’intersection fictive.
Symb : (AB)
Voir DISTANCE FICTIVE D’UN SEGMENT CAPABLE.
SEGMENT DISTANCE (RELATIF A UN POINT « A ») (l.m.)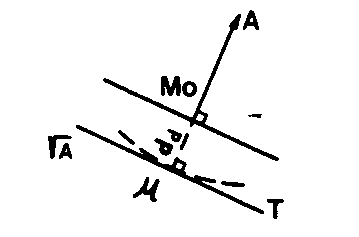
Dans un graphique destiné à déterminer le point définitif M d’une MULTILATÉRATION -2,6- , tangente m T à l’arc de cercle de centre A et de rayon Da = AM, distance observée au distancemètre et perpendiculaire à la direction AMo (Mo point approché).
Symb : G A
Mom est le DÉPLACEMENT DU SEGMENT DISTANCE.
Mom = dd = DA – DACalc
SEGMENTS CAPABLES lNDÉPENDANTS (l.m.)
Segments capables dont aucun ne peut être conclu à partir des autres.
SENSIBILITÉ D’UN SEGMENT CAPABLE (l.f.)
Déplacement latéral d’un SEGMENT CAPABLE pour une variation donnée de l’angle de relèvement, égale en général à 0,1 mgon.
s (cm) = 0,157 Df (km)
Df est la DISTANCE FICTIVE DU SEGMENT CAPABLE.
SENSIBILITÉ D’UNE VISÉE D’INTERSECTION (l.f.)
Déplacement latéral d’une visée d’intersection pour une variation donnée du gisement de celle-ci, variation prise, en général, égale à 0,1 mgon.
s (cm) = 0,157 D (km)
STATION LIBRE (CALCUL D’UNE) (l.m.)
Voir la définition de la STATION LIBRE -3,7-.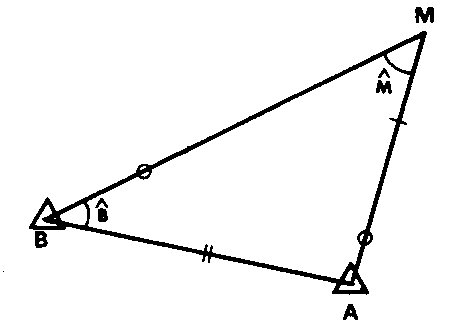
Points connus A et B,
Éléments observes : M et AM. On calcule la distance AB à partir des coordonnées de A et de B , puis l’angle B par la relation des sinus :
On obtient 2 déterminations de l’angle B (valeurs supplémentaires) ; un bon croquis permet de choisir la détermination convenable.
On est amené ensuite à résoudre l’intersection à partir- des coordonnées de A et B connaissant l’angle B. et l’angle  = 200 gon – B- M.
Le procédé ne comporte pas de vérification.