ALTÉRATION LINÉAIRE (COEFFICIENT, CORRECTION D’)
Voir COEFFICIENT et CORRECTION D’ALTÉRATION LINÉAIRE
COEFFICIENT D’ALTÉRATION LINÉAIRE (l.m.)
Dans un SYSTÈME DE PROJECTION CONFORME, quantité relative, quotient de la différence entre une longueur en projection « Dr »et son homologue sur l’ellipsoïde « Do », par la longueur « Do » sur l’ellipsoïde :![]() C’est la correction à apporter aux longueurs mesurées sur l’ellipsoïde, ramenée a l’unité de longueur.
C’est la correction à apporter aux longueurs mesurées sur l’ellipsoïde, ramenée a l’unité de longueur.
Le quotient mr = Dr/Do est le MODULE DE RÉDUCTION À LA PROJECTION. On a : kr = mr – 1
Dans une projection conforme, mr et kr sont indépendants de l’orientation de l’élément de longueur considéré.
Cas du SYSTÈME DE PROJECTION LAMBERT FRANCE :
Si on désigne par b la distance d’un point en projection au PARALLÈLE ORIGINE de la projection, on a :
* avant RÉDUCTION D’ÉCHELLE :![]() * après RÉDUCTION D’ÉCHELLE :
* après RÉDUCTION D’ÉCHELLE :
kr » k’r – 12.10-6
Pour les 3 zones Lambert France continentale, kr varie entre :
– 12.10-5 et + 37.10-5 c’est-à-dire -12 cm/km et + 37 cm/km
CONSTANTE X, CONSTANTE Y DANS LE SYSTÈME DE PROJECTION LAMBERT FRANCE (l.f. )
CONSTANTE X:
Après avoir défini l’axe des Y du SYSTÈME DE PROJECTION LAMBERT FRANCE comme étant la transformée du méridien origine méridien de Paris), au lieu de lui affecter la valeur X = 0, on lui affecte l’abscisse Cte X, telle qu’aucun point du territoire n’ait d’abscisse négative.
* Pour les trois zones Lambert I, II, III : Cte X = 600 000, 00 m
* Pour la zone Lambert Corse (IV) : Cte X = 234 358,00 m
CONSTANTE Y :
Après avoir défini le parallèle origine de chacun des quatre systèmes de projection Lambert France, on affecte à la tangente à ce parallèle, au point où il rencontre le méridien de Paris, une ordonnée désignée par Cte Y. Son rôle est double : éviter des ordonnées négatives et permettre par le chiffre des milliers de km, de différencier les quatre zones Lambert France.
* Zone Lambert I : Cte Y = 1 200 km = 1 200 000, 00 m
* Zone Lambert II : Cte Y = 2 200 km = 2 200 000, 00 m (voir SYSTÈME DE PROJECTION LAMBERT ÉTENDU)
* Zone Lambert III : Cte Y = 3 200 km = 3 200 000 m
* zone Lambert IV : Cte Y = 4 185,861369 km = 4 185 861,369 m
CONVERGENCE DU MÉRIDIEN D’UN LIEU AVEC LE MÉRIDIEN ORIGINE EN PROJECTION LAMBERT (l.f.)
Angle que fait le méridien d’un lieu A de longitude l par rapport au méridien origine (en France, Méridien de Paris).
Symbole : g 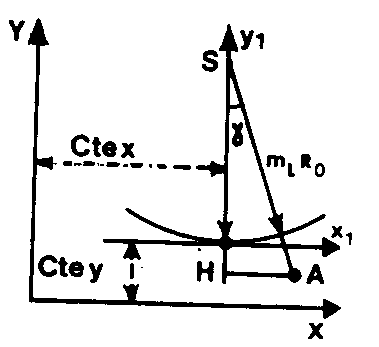 g = l sin j 0 (j 0, latitude du parallèle origine)
g = l sin j 0 (j 0, latitude du parallèle origine)
Si XA, YA sont les coordonnées Lambert de A, on définit :
x1(A) = XA – Cte x
y1(A) = YA – Cte y![]() mL est le module de RÉDUCTION D’ÉCHELLE.
mL est le module de RÉDUCTION D’ÉCHELLE.
Pour la France, les valeurs de mLRo sont données à SYSTÈME DE PROJECTION LAMBERT FRANCE.
CORRECTION D’ALTÉRATION LINÉAIRE (l.f.)
Dans un SYSTÈME DE PROJECTION CONFORME, quantité Cr qu’il faut ajouter à la distance D0 sur l’ellipsoïde pour obtenir la distance Dr en projection :
Dr = D0 + Cr et Cr = kr D0
LATITUDE ISOMÉTRIQUE (l.f.)
Expression transcendante de la latitude j intervenant dans les SYSTÈME DE PROJECTION CONFORMES de l’ellipsoïde. ![]() Voir expression de r et de N à RAYONS DE COURBURE PRINCIPAUX DE L’ELLIPSOÏDE DE RÉVOLUTION.
Voir expression de r et de N à RAYONS DE COURBURE PRINCIPAUX DE L’ELLIPSOÏDE DE RÉVOLUTION.
L’expression de la latitude isométrique est :![]() ln : logarithme népérien
ln : logarithme népérien
e : excentricité de l’ellipsoïde (voir ELLIPSOÏDE DE RÉFÉRENCE – 1,1 – ).
MÉRIDIEN ORIGINE (EN PROJECTION UTM) (l.m.)
Méridien sur lequel les longueurs de l’ellipsoïde sont conservées dans le SYSTÈME DE PROJECTION UTM avant RÉDUCTION D’ÉCHELLE.
MODULE DE RÉDUCTION À LA PROJECTION (l.m.)
Dans une projection conforme, quotient entre une distance en projection Dr, et la distance homologue sur l’ellipsoïde Do.![]() Le module est indépendant de l’orientation de l’élément de longueur considéré. Voir ALTÉRATION LINÉAIRE.
Le module est indépendant de l’orientation de l’élément de longueur considéré. Voir ALTÉRATION LINÉAIRE.
Dans un SYSTÈME DE PROJECTION LAMBERT, on calcule le module de réduction a la projection après RÉDUCTION D’ÉCHELLE en un point de latitude j par :![]() – où R a subi la RÉDUCTION D’ÉCHELLE (voir expression de R à RAYON DE PARALLÈLE EN PROJECTION LAMBERT)
– où R a subi la RÉDUCTION D’ÉCHELLE (voir expression de R à RAYON DE PARALLÈLE EN PROJECTION LAMBERT)
– j 0 latitude du parallèle origine de la zone Lambert considérée.![]() Pour le SYSTÈME DE PROJECTION LAMBERT FRANCE, voir les valeurs de :
Pour le SYSTÈME DE PROJECTION LAMBERT FRANCE, voir les valeurs de :
– « a » et de « e² » à ELLIPSOÏDE DE RÉFÉRENCE -1,1-
– j LATITUDE GÉODÉSIQUE -3,5- du lieu considéré.
On peut aussi calculer mr par mr = 1 + kr , kr étant le COEFFICIENT D’ALTÉRATION LINÉAIRE.
PARALLÈLE ORIGINE (EN PROJECTION LAMBERT) (l.m.)
Parallèle sur lequel les longueurs de l’ellipsoïde sont conservées dans le SYSTÈME DE PROJECTION LAMBERT avant RÉDUCTION D’ÉCHELLE.
RAYON DE COURBURE NORMAL DE L’ELLIPSOÏDE DANS UNE DIRECTION (l.m.)
Rayon de courbure de la section normale de l’ellipsoïde contenant la direction considérée.
Symb : RN
On l’obtient en toute rigueur par la relation d’Euler :![]() r et N, rayons de courbure principaux de l’ellipsoïde ; Az, azimut de la direction considérée .
r et N, rayons de courbure principaux de l’ellipsoïde ; Az, azimut de la direction considérée .
Pour les applications topographiques, il est en général suffisant de prendre pour RN la valeur : 6367 km.
RAYON DE PARALLÈLE EN PROJECTION LAMBERT (l.m.)
Soit mLRo le rayon du PARALLÈLE ORIGINE de la projection après RÉDUCTION D’ÉCHELLE, j o la latitude de ce parallèle origine, L la LATITUDE ISOMÉTRIQUE pour la latitude j , Lo son expression pour latitude j o : l’expression du rayon R d’un parallèle de latitude j en projection Lambert s’exprime par :
R = mLRo e-sin j o (L – Lo)
e : base des logarithmes népériens, tel que ln e=1
RAYONS DE COURBURE PRINCIPAUX DE L’ELLIPSOÏDE DE RÉVOLUTION (l.m.)
Rayons de courbure principaux au sens d’Euler : ce sont :
* le rayon de courbure de la section méridienne de l’ellipsoïde :![]() (j LATITUDE GÉODÉSIQUE -3,6- du lieu)
(j LATITUDE GÉODÉSIQUE -3,6- du lieu)
* le segment de normale comprise entre l’ellipsoïde et l’axe de révolution :![]() Voir les valeurs de « a » et de « e2 » pour l’ellipsoïde de Clarke à ELLIPSOÏDE DE RÉFÉRENCE -1,1-.
Voir les valeurs de « a » et de « e2 » pour l’ellipsoïde de Clarke à ELLIPSOÏDE DE RÉFÉRENCE -1,1-.
RÉDUCTION ANGULAIRE À LA CORDE (CORRECTION DE) (l.f.)
Correction angulaire qu’il y a lieu d’apporter aux observations azimutales d’un tour d’horizon, pour que dans le système de projection utilisé, les transformées des courbes de visée soient ramenées à la corde. Les transformations des courbes de visée, (que l’on peut assimiler à des transformées de lignes géodésiques de l’ellipsoïde), tournent toujours leur concavité vers le PARALLÈLE ORIGINE EN PROJECTION LAMBERT ou vers le MÉRIDIEN ORIGINE EN PROJECTION UTM.
Symb. : rc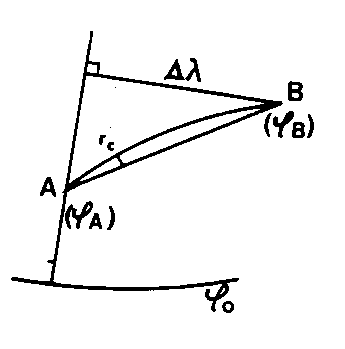
Pour la projection Lambert :
rc (mgon) = 0,1 m 1/3 D l (km)
m est une expression complexe de la latitude, tabulée par l’IGN. On entre dans cette table avec l’argument j 1/3 ,c’est-à-dire la latitude du point situé au tiers de l’arc AB.
D l est l’expression en km, de la différence de longitude entre A et B.
RÉDUCTION D’ÉCHELLE, MODULE DE RÉDUCTION D’ÉCHELLE :
* RÉDUCTION ÉCHELLE (l.f.)
Après. avoir défini un système de représentation, artifice consistant à multiplier le module initial de réduction à la projection par un facteur constant mL, appelé MODULE DE RÉDUCTION D’ÉCHELLE, ce qui diminue le COEFFICIENT D’ALTÉRATION LINÉAIRE en valeur absolue.
* MODULE DE RÉDUCTION D’ÉCHELLE (l.m.)
Facteur constant par lequel on multiplie le MODULE initial DE RÉDUCTION A LA PROJECTION.
Symbole mL
Voir les valeurs adoptées pour mL en France à SYSTÈME DE PROJECTION LAMBERT FRANCE.
RÉDUCTION DE LONGUEUR À LA PROJECTION (l.f.)
Action d’apporter à une longueur sur l’ellipsoïde de référence, la correction nécessaire pour avoir la longueur en projection.
Voir MODULE DE RÉDUCTION À LA PROJECTION
RÉDUCTION LINÉAIRE À LA CORDE (CORRECTION DE)
Correction toujours négative, qui ramène la longueur d’un arc de courbe à la corde qui la sous-tend.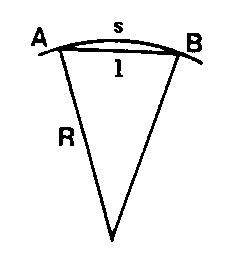 Si s = AB (arc) et l = AB (corde) et R le rayon de courbure moyen entre A et B, on a :
Si s = AB (arc) et l = AB (corde) et R le rayon de courbure moyen entre A et B, on a :![]() En topographie, la correction qui ramène la longueur d’une visée affectant la courbure terrestre à la corde qui la sous-tend est toujours négligeable.
En topographie, la correction qui ramène la longueur d’une visée affectant la courbure terrestre à la corde qui la sous-tend est toujours négligeable.
SYSTÈME DE PROJECTION CONFORME (l.m.)
SYSTÈME DE PROJECTION -1,1- qui conserve les angles et où le MODULE DE RÉDUCTION À LA PROJECTION a une valeur indépendante du gisement considéré.
En géodésie et topographie, on utilise exclusivement des systèmes de projection conformes : les plus utilises sont le SYSTÈME DE PROJECTION LAMBERT et le SYSTÈME DE PROJECTION UTM.
SYSTÈME DE PROJECTION LAMBERT (l.m.)
SYSTÈME DE PROJECTION CONFORME conique de l’ellipsoïde de référence sur le plan, dit plan de projection.
Les méridiens sont représentes par des droites qui convergent en un point du méridien origine de la projection. Voir CONVERGENCE DU MÉRIDIEN D’UN LIEU
SYSTÈME DE PROJECTION LAMBERT FRANCE (l.m.)
SYSTÈME DE PROJECTION LAMBERT, officiel en France, institué par note du Service Géographique de l’Armée du l0 Août 1920 et mis en application le 15 Mars 1922. Il est utilisé pour la détermination des coordonnées des points géodésiques de la NOUVELLE TRIANGULATION DE LA FRANCE -5,1-.
Le méridien origine est celui de Paris.
Pour réduire au maximum les ALTÉRATIONS LINÉAIRES, le territoire français a été divisé en 4 zones Lambert dont les PARALLÈLES ORIGINES j 0 et les caractéristiques sont les suivantes :

mL est le MODULE DE RÉDUCTION D’ÉCHELLE. Pour les trois zones Lambert de la France continentale, il eût en général suffisant de prendre la valeur mL = 1 – 12.10-5 = 0,99988
R est le RAYON DE PARALLÈLE EN PROJECTION LAMBERT donné par :
R = mLRo e-sin j o (L – Lo)
e : base des logarithmes népériens, tel que ln e=1
Selon la zone Lambert considérée, mL, R0 et j 0 ont les valeurs du tableau ci-dessus.
L est calculé par la formule indiquée à LATITUDE ISOMÉTRIQUE.
Voir aussi CONSTANTE X et CONSTANTE Y DANS LE SYSTÈME DE PROJECTION LAMBERT FRANCE et CONVERGENCE DU MÉRIDIEN D’UN LIEU.
SYSTÈME DE PROJECTION LAMBERT II ÉTENDU (l.m.)
La généralisation de l’informatique et l’utilisation de banques de données s’accommodent mal de quatre zones Lambert. Aussi adopte-t-on, pour les fichiers, un système de projection Lambert II étendu qui constitue un référentiel unique pour toute la France.
SYSTÈME DE PROJECTION U.T.M. (l.m.)
Le système de représentation de Mercator Transverse Universel est une projection conforme de l’ellipsoïde de référence (généralement ellipsoïde international), sur le plan de projection par fuseaux de 6° de différence de longitude (60 fuseaux) : 3° de par et d’autre d’un MÉRIDIEN ORIGINE :
* Le fuseau No 30 a pour méridien origine : l 0 = 3° Ouest Greenwich
* Le fuseau No 31 a pour méridien origine : l 0 = 3° Est Greenwich
* Le fuseau No 32 a pour méridien origine : l 0 = 9° Ouest Greenwich
Le système est universel, parce que les formules de transformation de coordonnées géographiques en coordonnées rectangulaires établies pour un des fuseaux sont valables pour les 59 autres fuseaux. Dans chaque fuseau, l’origine des coordonnées est l’intersection du MÉRIDIEN ORIGINE et de l’équateur, ce point ayant pour coordonnées :
X = E = 500 000 m (Cte X)
Y = N = 0 dans l’hémisphère Nord
Y = N = 10 000 000 m dans l’hémisphère Sud
TRANSFORMATION DE COORDONNÉES GÉOGRAPHIQUES (l ,j) EN COORDONNÉES LAMBERT (X,Y) (CALCULS DE)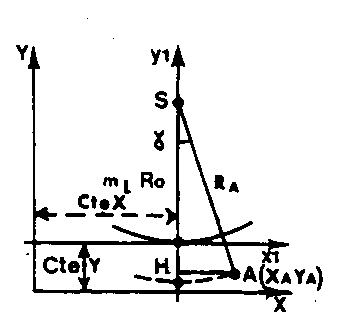
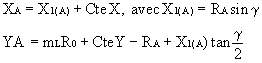
g est la CONVERGENCE DU MÉRIDIEN DU LIEU AVEC LE MÉRIDIEN ORIGINE -10,1-.
g = l A sin j 0
Pour la France, voir SYSTÈME DE PROJECTION LAMBERT FRANCE où l’on trouvera la formule permettant le calcul de R en fonction de j , les valeurs de mLR0 et de j 0 selon la zone Lambert considérée ; l A est la longitude du point considéré A par rapport au méridien de Paris. Voir aussi CONSTANTE X CONSTANTE Y DANS LE SYSTÈME DE PROJECTION LAMBERT FRANCE.
TRANSFORMATION DE COORDONNÉES LAMBERT FRANCE EN COORDONNÉES GÉOGRAPHIQUES (l.f.)
Les calculs de la transformation des coordonnées Lambert France XA, YA, en coordonnées géographiques l A, j A, nécessitent le calcul préalable de l’angle g CONVERGENCE DU MÉRIDIEN DU LIEU avec LE MÉRIDIEN ORIGINE :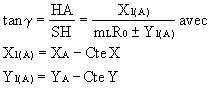
Voir CONSTANTE X, CONSTANTE Y DANS LE SYSTÈME DE PROJECTION LAMBERT FRANCE.
De la valeur de g on déduit :
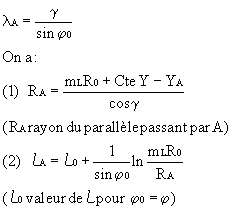
Dans le deuxième membre de (2), on remplace RA par sa valeur (l) ; ce deuxième membre a alors une valeur connue K . On introduit une valeur approchée de j dans LA (voir expression à LATITUDE ISOMÉTRIQUE puis, une série de valeurs récurrentes de j jusqu’à ce que LA converge vers K. On obtient ainsi la valeur cherchée de j A.
