INTERVALLE LINÉAIRE D’IMPLANTATION (l.m.)
Sur une courbe à implanter, intervalle d’arc de courbe séparant deux points consécutifs.
Symb. : i_L

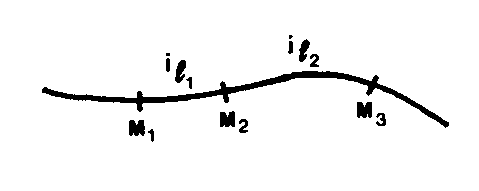
M₁M₂ = i_L1
M₂M₃ = i_L2
En général, les points M₁, M₂, M₃, etc. sont pris suffisamment rapprochés pour que l’intervalle d’arc de courbe soit assimilable à la corde :
arc M₁M₂ = corde M₁M₂
arc M₂M₃ = corde M₂M₃
S’il n’en est pas ainsi, il y a lieu de distinguer l’intervalle linéaire curviligne d’implantation de l’intervalle linéaire rectiligne d’implantation.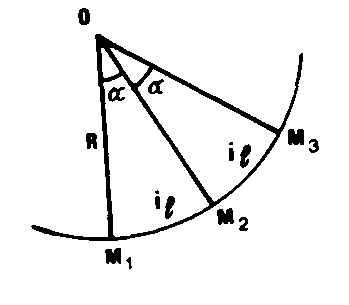Pour un arc de cercle de rayon R , l’intervalle linéaire d’implantation est constant lorsque l’INTERVALLE ANGULAIRE D’IMPLANTATION est constant i_L = R. a (radian)